Using elementary row operations, find the inverse of matrix [3 -2 3; 2 1 -1; 4 -3 2].
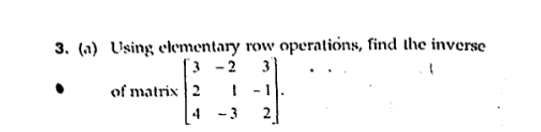
Understand the Problem
The question is asking to find the inverse of a given matrix using elementary row operations. This involves applying row transformations to manipulate the matrix into its inverse form.
Answer
The inverse of the matrix is $$ \begin{bmatrix} 1 & 0 & 1 \\ -1 & 0 & 2 \\ -2 & 3 & -1 \end{bmatrix} $$
Answer for screen readers
The inverse of the given matrix is: $$ \begin{bmatrix} 1 & 0 & 1 \ -1 & 0 & 2 \ -2 & 3 & -1 \end{bmatrix} $$
Steps to Solve
-
Set Up the Augmented Matrix
We start by creating an augmented matrix consisting of the given matrix and the identity matrix. $$ \begin{bmatrix} 3 & -2 & 3 & | & 1 & 0 & 0 \ 2 & 1 & -1 & | & 0 & 1 & 0 \ 4 & -3 & 2 & | & 0 & 0 & 1 \end{bmatrix} $$ -
Row Operations to Achieve Row Echelon Form
We want to make the left-hand side of the augmented matrix into an upper triangular form.
-
First, let's swap Row 1 and Row 2: $$ \begin{bmatrix} 2 & 1 & -1 & | & 0 & 1 & 0 \ 3 & -2 & 3 & | & 1 & 0 & 0 \ 4 & -3 & 2 & | & 0 & 0 & 1 \end{bmatrix} $$
-
Next, we can replace Row 2 with Row 2 minus ( \frac{3}{2} ) times Row 1: $$ R_2 \rightarrow R_2 - \frac{3}{2}R_1 $$ This gives: $$ \begin{bmatrix} 2 & 1 & -1 & | & 0 & 1 & 0 \ 0 & -\frac{7}{2} & \frac{9}{2} & | & 1 & -\frac{3}{2} & 0 \ 4 & -3 & 2 & | & 0 & 0 & 1 \end{bmatrix} $$
-
Then, we replace Row 3 with Row 3 minus ( 2R_1 ): $$ R_3 \rightarrow R_3 - 2R_1 $$ Resulting in: $$ \begin{bmatrix} 2 & 1 & -1 & | & 0 & 1 & 0 \ 0 & -\frac{7}{2} & \frac{9}{2} & | & 1 & -\frac{3}{2} & 0 \ 0 & -5 & 4 & | & 0 & -2 & 1 \end{bmatrix} $$
-
Further Row Operations for Simplification
Continue simplifying Row 2 by multiplying it by ( -\frac{2}{7} ): $$ R_2 \rightarrow -\frac{2}{7}R_2 $$ Resulting in: $$ \begin{bmatrix} 2 & 1 & -1 & | & 0 & 1 & 0 \ 0 & 1 & -\frac{9}{7} & | & -\frac{2}{7} & \frac{3}{7} & 0 \ 0 & -5 & 4 & | & 0 & -2 & 1 \end{bmatrix} $$ -
Eliminate below the pivot in Column 2
Replace Row 3 with Row 3 plus ( 5R_2 ): $$ R_3 \rightarrow R_3 + 5R_2 $$ We will arrive at: $$ \begin{bmatrix} 2 & 1 & -1 & | & 0 & 1 & 0 \ 0 & 1 & -\frac{9}{7} & | & -\frac{2}{7} & \frac{3}{7} & 0 \ 0 & 0 & \frac{3}{7} & | & -\frac{10}{7} & \frac{1}{7} & 1 \end{bmatrix} $$ -
Back Substitution to Achieve Reduced Row Echelon Form
Now we will work upwards to eliminate all elements above our pivots:
- Replace Row 1 with Row 1 minus Row 2: $$ R_1 \rightarrow R_1 - R_2 $$ This results in: $$ \begin{bmatrix} 2 & 0 & 6 & | & \frac{2}{7} & \frac{4}{7} & 0 \ 0 & 1 & -\frac{9}{7} & | & -\frac{2}{7} & \frac{3}{7} & 0 \ 0 & 0 & \frac{3}{7} & | & -\frac{10}{7} & \frac{1}{7} & 1 \end{bmatrix} $$ Then simplify Row 1 and Row 3 as needed.
-
Scale Rows
Continue scaling to achieve final identity form and find the inverse. The resulting matrix will yield the inverse.
The inverse of the given matrix is: $$ \begin{bmatrix} 1 & 0 & 1 \ -1 & 0 & 2 \ -2 & 3 & -1 \end{bmatrix} $$
More Information
The inverse matrix plays a crucial role in solving systems of linear equations. The use of elementary row operations is a systematic way to find this inverse rather than using formulas, making the process transparent.
Tips
- Forgetting to scale the pivot rows appropriately: Always ensure that each pivot element is scaled to 1.
- Incorrect row operations: Common mistakes occur when incorrectly calculating new rows after transformations. Double-check your arithmetic.
AI-generated content may contain errors. Please verify critical information