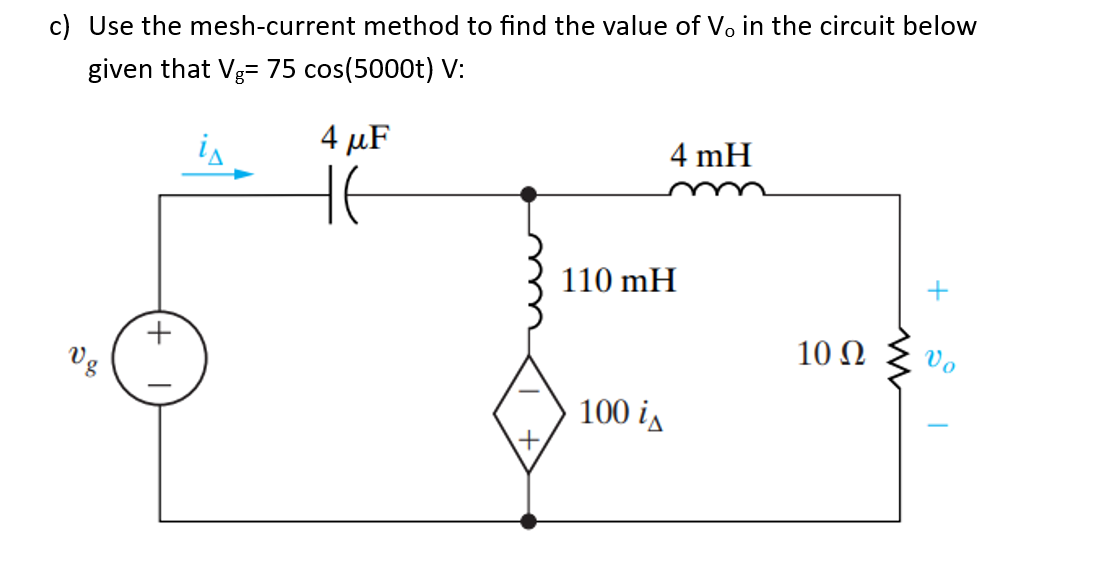
Use the mesh-current method to find the value of Vo in the circuit below given that Vg= 75 cos(5000t) V:

Steps to Solve

1. Identify the Mesh Currents

Define the mesh currents in the circuit. Let $i_1$ represent the current flowing clockwise in the left mesh, and let $i_2$ represent the current flowing in the right mesh. The current leaving the voltage source is $i_{\Delta} = i_1 - i_2$.

2. Write the Mesh Equations

Using Kirchhoff's Voltage Law (KVL), apply it to both meshes:

For mesh 1 (left):

$$ -V_g + \left( \frac{1}{j\omega C} \cdot i_1 \right) + j\omega L_{1} i_1 + j\omega L_{2} (i_1 - i_2) = 0 $$

For mesh 2 (right):

$$ j\omega L_{3} (i_2 - i_1) + R \cdot i_2 + 100 i_{\Delta} = 0 $$

Where:

• $L_1 = 4 , mH = 4 \times 10^{-3} , H$
• $L_2 = 110 , mH = 110 \times 10^{-3} , H$
• $L_3 = 4 , mH = 4 \times 10^{-3} , H$
• $C = 4 , \mu F = 4 \times 10^{-6} , F$
• $R = 10 , \Omega$
• $\omega = 5000$ (given by $vg = 75 \cos(5000t)$).

3. Substitute Values and Solve the System of Equations

Substitute the component values into the mesh equations:

From mesh 1:

$$ -V_g + \frac{1}{j(5000)(4 \times 10^{-6})}i_1 + j(5000)(4 \times 10^{-3})i_1 + j(5000)(110 \times 10^{-3})(i_1 - i_2) = 0 $$

And for mesh 2:

$$ j(5000)(4 \times 10^{-3})(i_2 - i_1) + 10i_2 + 100(i_1 - i_2) = 0 $$

From the first mesh equation, we substitute $V_g = 75 \cos(5000t)$ and simplify.

4. Calculate the Voltage Vo

Once you’ve obtained expressions for $i_1$ and $i_2$, you can calculate $V_o$ across the 10 Ω resistor:

$$ V_o = R \cdot i_2 = 10 i_2 $$

Substitute the calculated $i_2$ value back to determine the desired voltage.