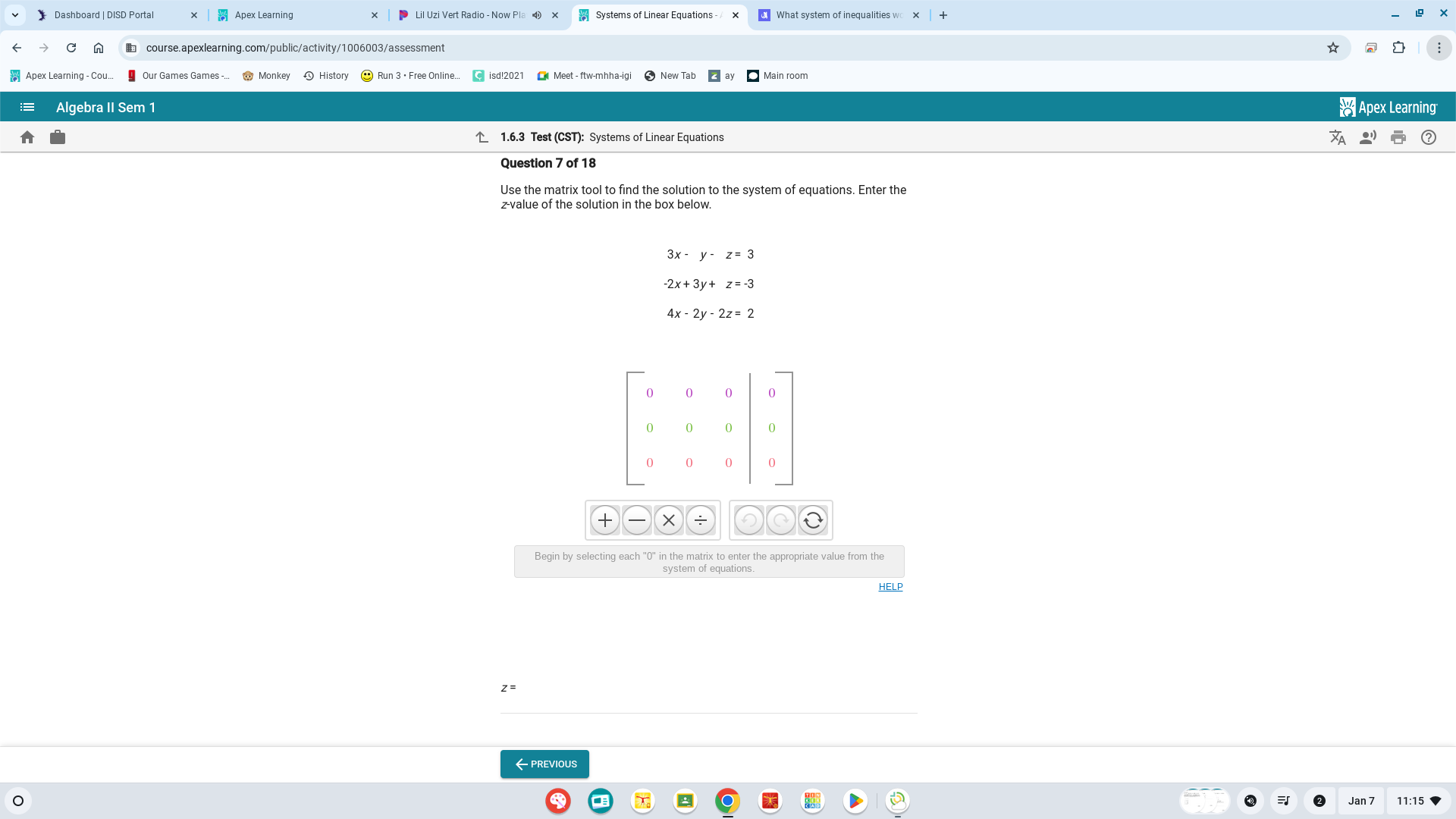
Use the matrix tool to find the solution to the system of equations. Enter the z-value of the solution in the box below.

Steps to Solve

1. Write the equations in matrix form
   We can express the system of equations in augmented matrix form: $$ \begin{bmatrix} 3 & -1 & -1 & | & 3 \ -2 & 3 & 1 & | & -3 \ 4 & -2 & -2 & | & 2 \end{bmatrix} $$

2. Use Gaussian elimination
   We perform row operations to get the matrix in row-echelon form.

   • Start with the first row: $R_1: \begin{bmatrix} 3 & -1 & -1 | 3 \end{bmatrix}$.
   • Make the first element of the second row a zero by row operation: (R_2 = R_2 + \frac{2}{3}R_1): $R_2: \begin{bmatrix} 0 & \frac{7}{3} & -\frac{1}{3} | 1 \end{bmatrix}$.
   • Next, eliminate below the $R_1$: (R_3 = R_3 - \frac{4}{3}R_1): $R_3: \begin{bmatrix} 0 & -\frac{2}{3} & -\frac{2}{3} | -2 \end{bmatrix}$.

3. Continuing Gaussian elimination
   Next, simplify (R_3) using (R_2):

   • Multiply (R_2) by $3$ to eliminate fractions:
     $R_2: \begin{bmatrix} 0 & 7 & -1 | 3 \end{bmatrix}$.
   • Scale: (R_3 + \frac{2}{7}R_2):
     $R_3: \begin{bmatrix} 0 & 0 & -1 | -1 \end{bmatrix}$.

4. Back substitution
   Convert this matrix back into system of equations: $$ z = 1 $$ From (R_2): $y = \frac{3 + z}{7} = \frac{3 + 1}{7} = \frac{4}{7}$ From (R_1): $3x - y - 1 = 3 \rightarrow x = 2$.

5. Identify the z-value
   The solution to the system requires the value of $z$ which is 1.