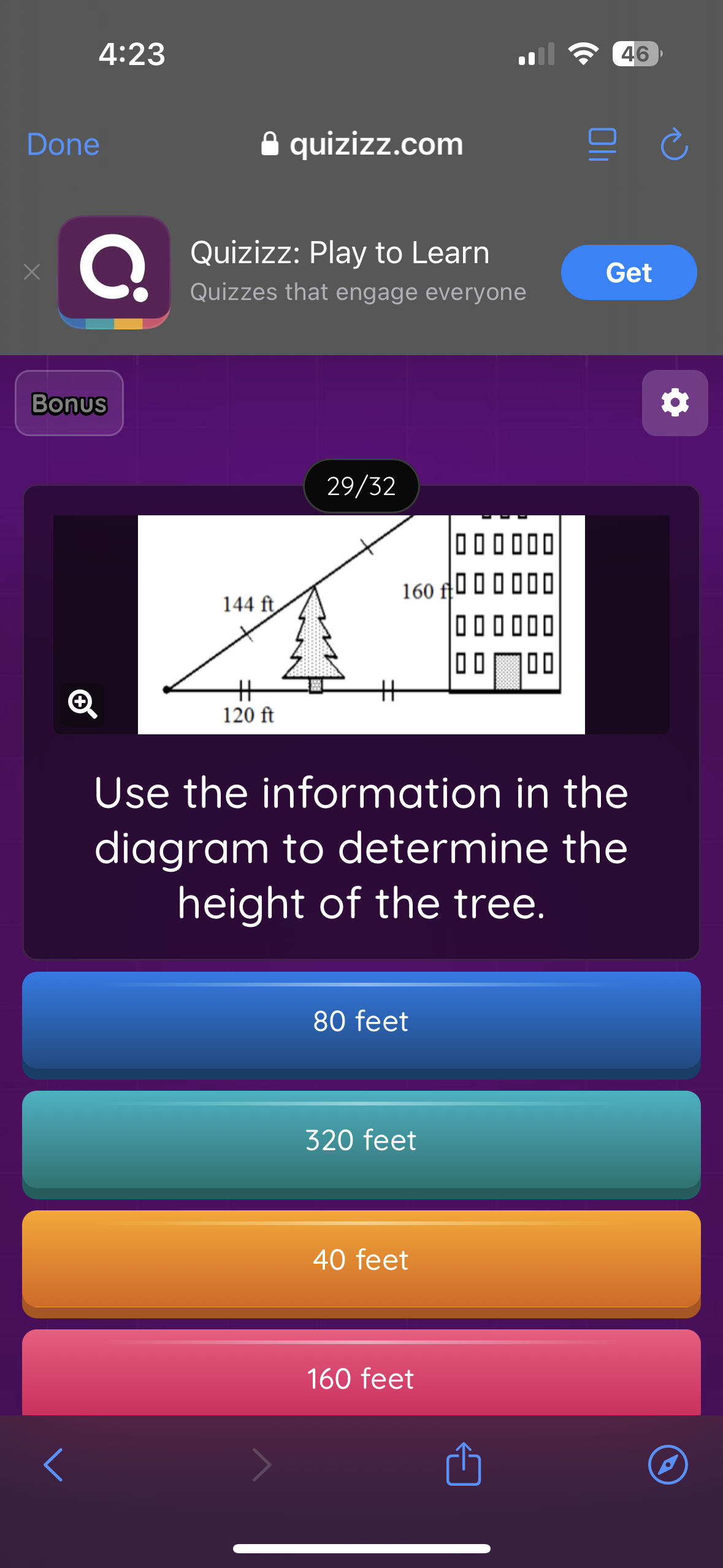
Use the information in the diagram to determine the height of the tree.

Steps to Solve

1. Identify the Right Triangle The diagram forms a right triangle with the tree height as one leg, the distance from the base of the tree to the building as the other leg, and the line from the top of the tree to the observer as the hypotenuse.

2. Label the Known Distances From the diagram:

• The distance from the tree to the building (horizontal leg) is given as 120 ft.
• The distance from the observer to the top of the tree (hypotenuse) is 144 ft.
• The vertical height of the building does not factor into the calculation for the tree height.

3. Apply the Pythagorean Theorem Using the Pythagorean theorem: $$ a^2 + b^2 = c^2 $$ Let ( a ) be the height of the tree, ( b = 120 ) ft, and ( c = 144 ) ft.

4. Set Up the Equation Substituting the known values into the equation: $$ a^2 + 120^2 = 144^2 $$

5. Calculate the Squares Calculate ( 120^2 ) and ( 144^2 ): $$ 120^2 = 14400 $$ $$ 144^2 = 20736 $$

6. Solve for ( a^2 ) Now, substituting the values: $$ a^2 + 14400 = 20736 $$ Rearranging gives: $$ a^2 = 20736 - 14400 $$

7. Calculate ( a^2 ) Perform the subtraction: $$ a^2 = 6336 $$

8. Find ( a ) Take the square root to find ( a ): $$ a = \sqrt{6336} $$

9. Calculate the Height Using a calculator: $$ a \approx 79.6 \text{ feet} $$