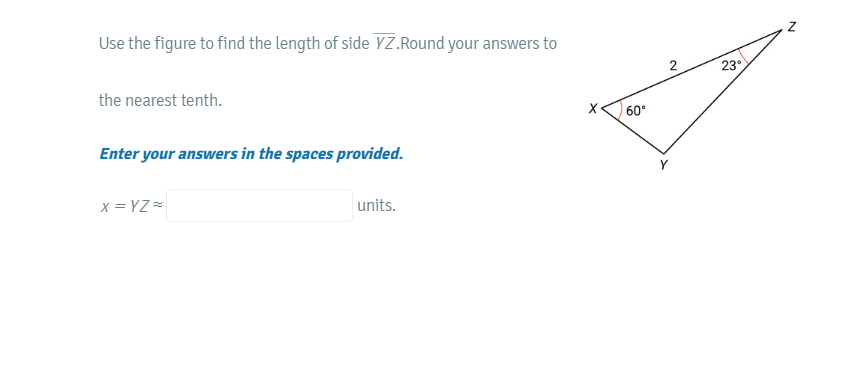
Use the figure to find the length of side YZ. Round your answer to the nearest tenth.

Steps to Solve

1. Identify known values We are given the following values from the triangle:

• Side length $XY = 2$ units
• Angle $\angle YXZ = 60^\circ$
• Angle $\angle XYZ = 23^\circ$

2. Calculate the missing angle To find angle $\angle YZ = \angle ZXY$, we can use the fact that the sum of angles in a triangle equals $180^\circ$: $$ \angle ZXY = 180^\circ - \angle YXZ - \angle XYZ $$ Substituting the known angle values: $$ \angle ZXY = 180^\circ - 60^\circ - 23^\circ = 97^\circ $$

3. Apply the Law of Sines The Law of Sines states that: $$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $$ We want to find side $YZ$, which is opposite angle $60^\circ$. Let $YZ = x$. Using the Law of Sines: $$ \frac{x}{\sin(60^\circ)} = \frac{2}{\sin(23^\circ)} $$

4. Solve for x Rearranging gives: $$ x = 2 \cdot \frac{\sin(60^\circ)}{\sin(23^\circ)} $$

5. Calculate the sine values Using sine values:

• $\sin(60^\circ) \approx 0.8660$
• $\sin(23^\circ) \approx 0.3907$

Substituting these values, we get: $$ x \approx 2 \cdot \frac{0.8660}{0.3907} $$

6. Final calculation Calculating: $$ x \approx 2 \cdot 2.215 = 4.430 $$

7. Round to the nearest tenth Rounding $4.430$ to the nearest tenth gives $4.4$.