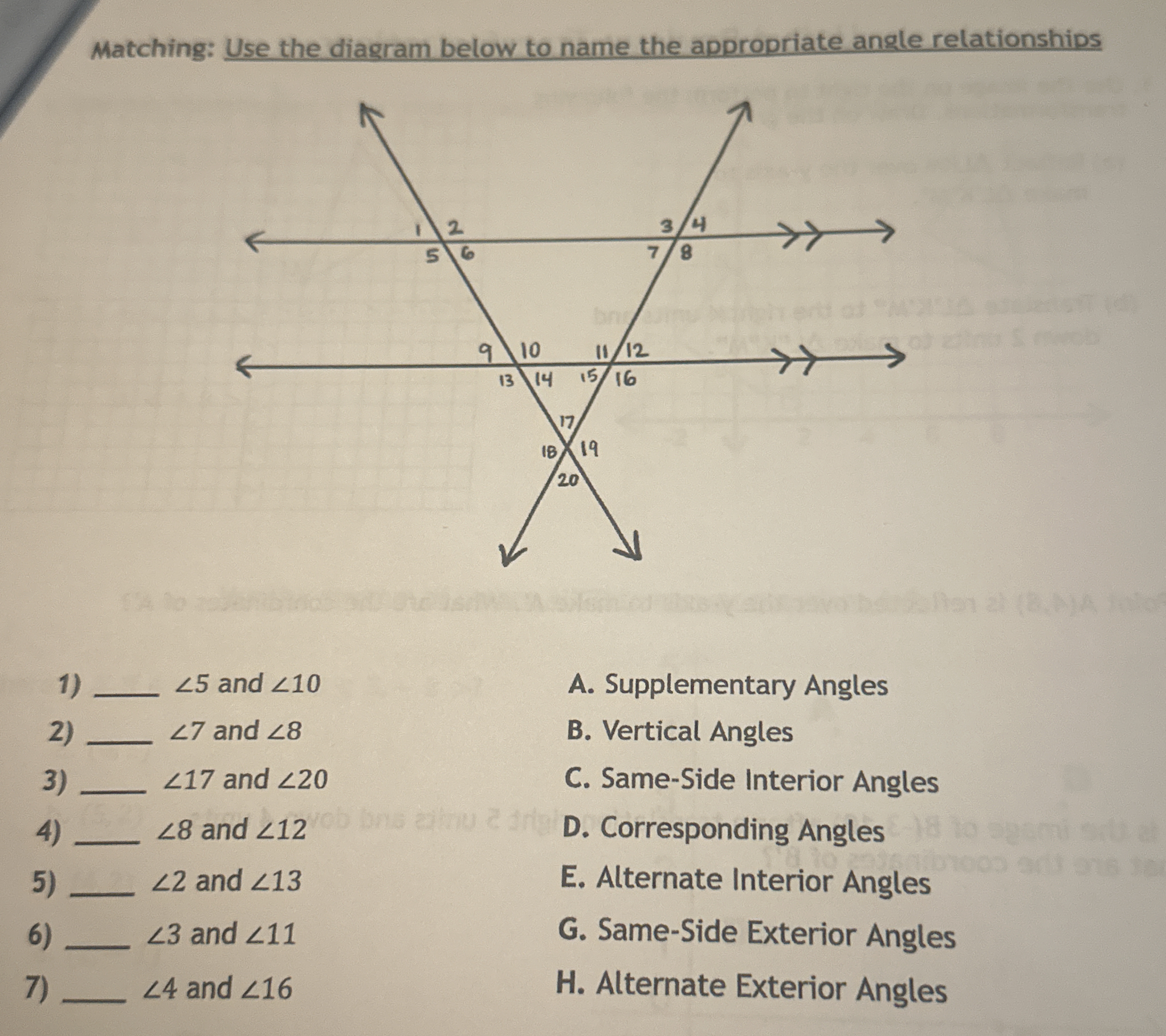
Use the diagram below to name the appropriate angle relationships.
Understand the Problem
The question is asking for the identification of angle relationships based on a diagram involving lines and angles labeled with numbers. The goal is to match pairs of angles with their corresponding relational terms from a provided list.
Answer
1) D 2) G 3) A 4) B 5) E 6) H 7) F
Answer for screen readers
- D. Corresponding Angles
- G. Same-Side Interior Angles
- A. Supplementary Angles
- B. Vertical Angles
- E. Alternate Interior Angles
- H. Same-Side Exterior Angles
- F. Alternate Exterior Angles
Steps to Solve
-
Identify Angle Relationships Look at the provided angles with numbers based on their position in relation to the two intersecting lines. Familiarize yourself with the angle relationship definitions.
-
Apply Definitions to Pairs of Angles For each pair given in the question, determine their relationship:
- Vertical Angles: Angles opposite each other when two lines intersect.
- Supplementary Angles: Two angles that add up to 180°.
- Same-Side Interior Angles: Angles on the same side of the transversal and between the lines.
- Corresponding Angles: Angles in the same position at each intersection where a transversal crosses two lines.
- Alternate Interior Angles: Angles on opposite sides of the transversal, inside the two lines.
- Same-Side Exterior Angles: Angles on the same side of the transversal but outside the two lines.
- Alternate Exterior Angles: Angles on opposite sides of the transversal, outside of the two lines.
-
Analyze Each Pair
- For (1): $\angle 5$ and $\angle 10$ → Corresponding angles.
- For (2): $\angle 7$ and $\angle 8$ → Same-side interior angles.
- For (3): $\angle 17$ and $\angle 20$ → Supplementary angles.
- For (4): $\angle 8$ and $\angle 12$ → Vertical angles.
- For (5): $\angle 2$ and $\angle 13$ → Alternate interior angles.
- For (6): $\angle 3$ and $\angle 11$ → Same-side exterior angles.
- For (7): $\angle 4$ and $\angle 16$ → Alternate exterior angles.
-
Match Each Pair with the Correct Terms Use the analysis to match each pair with corresponding relationship terms from the list provided.
- D. Corresponding Angles
- G. Same-Side Interior Angles
- A. Supplementary Angles
- B. Vertical Angles
- E. Alternate Interior Angles
- H. Same-Side Exterior Angles
- F. Alternate Exterior Angles
More Information
Understanding these angle relationships is essential in geometry, especially when working with parallel lines and transversals. It helps in solving various geometric proofs and problems.
Tips
- Mixing up vertical angles with corresponding angles; remember, vertical angles are opposite each other.
- Forgetting that supplementary angles must add up to 180°; always check the degree measures if available.
AI-generated content may contain errors. Please verify critical information