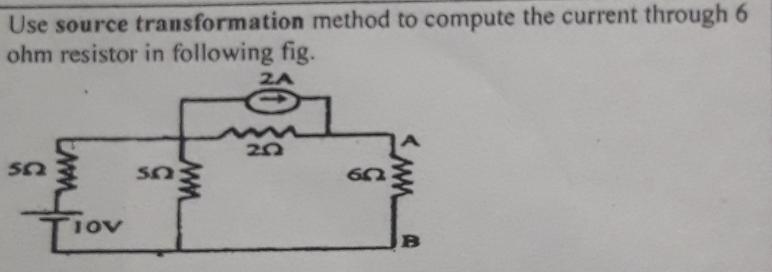
Use source transformation method to compute the current through 6 ohm resistor in the following fig.

Steps to Solve

1. Identify the components of the circuit

Identify the voltage source, current sources, resistors, and their values from the circuit diagram. Here, we have:

• A voltage source of $10 V$.
• A current source of $2 A$.
• Resistors with values $5 \Omega$, $2 \Omega$, and $6 \Omega$.

2. Transform the voltage source to a current source

Use the source transformation method. To transform the $10 V$ voltage source in series with a $5 \Omega$ resistor to a current source: $$ I = \frac{V}{R} = \frac{10 V}{5 \Omega} = 2 A $$ So, the voltage source can be represented as a $2 A$ current source in parallel with a $5 \Omega$ resistor.

3. Redraw the circuit with the transformed source

Now, we redraw the circuit replacing the $10 V$ source with the equivalent $2 A$ current source and a $5 \Omega$ resistor in parallel with it. This will create a new circuit arrangement.

4. Calculate the combined resistance in the circuit

Next, calculate total resistance seen by the $6 \Omega$ resistor. The $5 \Omega$ resistor is in parallel with the original $2 A$ current source.

The effective resistance $R_{eff}$ can be found using: $$ \frac{1}{R_{eff}} = \frac{1}{5 \Omega} + \frac{1}{2 \Omega} $$

5. Solve for the combined resistance

Calculate the effective resistance: $$ \frac{1}{R_{eff}} = \frac{1}{5} + \frac{1}{2} = \frac{2 + 5}{10} = \frac{7}{10} $$

So, $$ R_{eff} = \frac{10}{7} \Omega \approx 1.43 \Omega $$

6. Using current division to find the current through the $6 \Omega$ resistor

Using the current division rule: $$ I_{6\Omega} = I_{total} \cdot \frac{R_{parallel}}{R_{total}} $$

Where,

• $I_{total} = 2 A$ (the total current),
• $R_{parallel} = 6 \Omega$,
• $R_{total} = R_{eff} + 6 \Omega$.

Now, calculate total resistance: $$ R_{total} = \frac{10}{7} + 6 = \frac{10 + 42}{7} = \frac{52}{7} \Omega $$

Now substitute values: $$ I_{6\Omega} = 2 A \cdot \frac{6}{\frac{52}{7}} = 2 A \cdot \frac{6 \cdot 7}{52} = 2 A \cdot \frac{42}{52} = 2 A \cdot \frac{21}{26} $$

Finally calculate: $$ I_{6\Omega} \approx 1.615 A $$