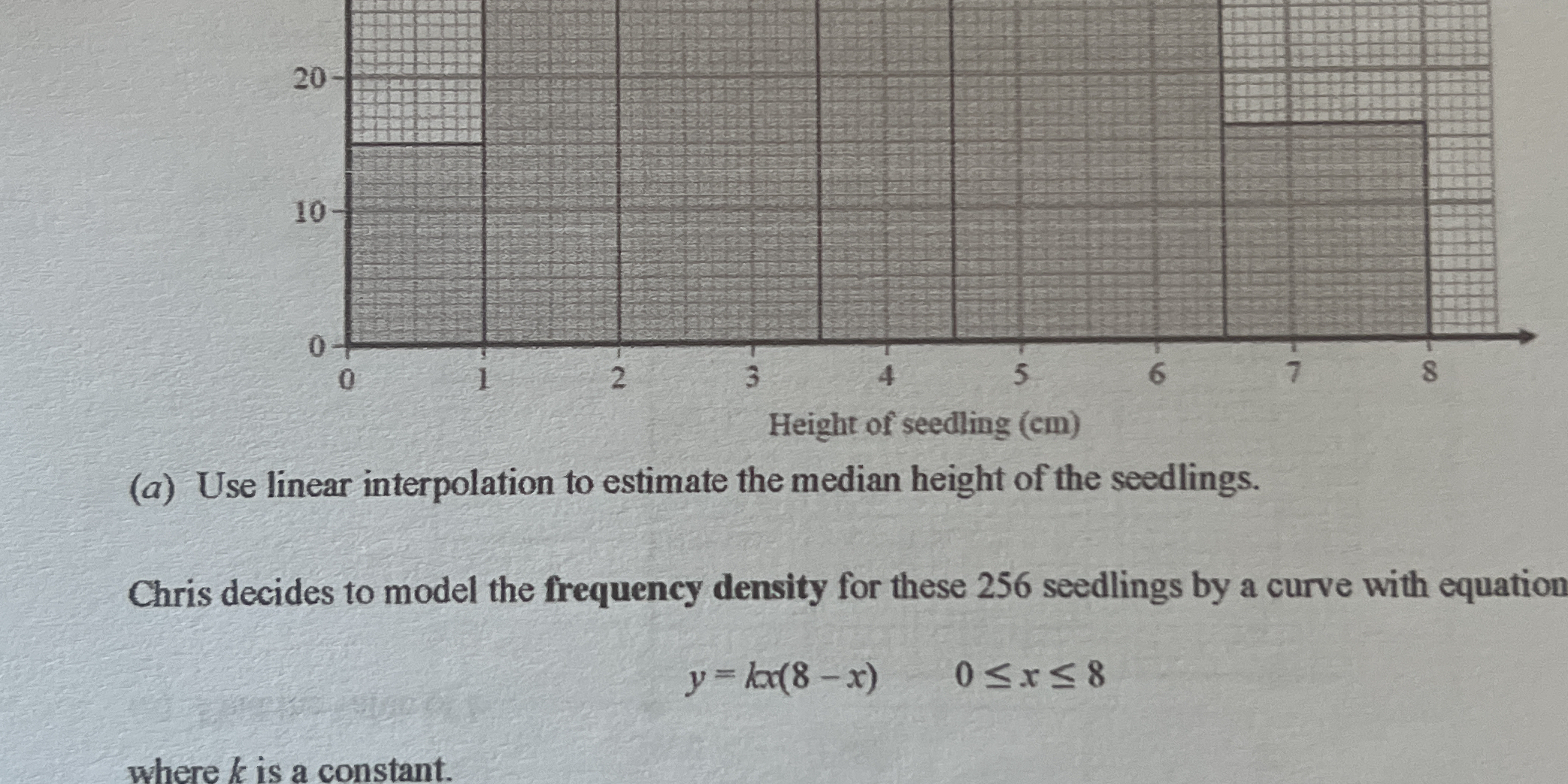
Use linear interpolation to estimate the median height of the seedlings.

Understand the Problem

The question is asking to use linear interpolation to estimate the median height of the seedlings based on the provided histogram of seedling heights. This involves finding the median value using the data represented in the graph.

Answer

The estimated median height of the seedlings is approximately $3.63$ cm.

Steps to Solve

Calculate Total Number of Seedlings The first step is to find the total number of seedlings represented in the histogram. Count the frequency (or height) of each bin of seedling heights and add them up.

For the heights given in the histogram:
- From 0 to 1 cm: 20 seedlings
- From 1 to 2 cm: 30 seedlings
- From 2 to 3 cm: 40 seedlings
- From 3 to 4 cm: 60 seedlings
- From 4 to 5 cm: 50 seedlings
- From 5 to 6 cm: 30 seedlings
- From 6 to 7 cm: 20 seedlings
- From 7 to 8 cm: 6 seedlings
Total = $20 + 30 + 40 + 60 + 50 + 30 + 20 + 6 = 256$ seedlings.
Find the Median Position The median is the middle value of a data set. Since there are 256 seedlings, the median position is given by:

$$\frac{256 + 1}{2} = 128.5$$

This means the median will be between the 128th and 129th seedlings.
Cumulative Frequency Calculation Next, calculate the cumulative frequency to determine where the 128th and 129th seedlings fall within the bins:
- Up to 1 cm: 20
- Up to 2 cm: 20 + 30 = 50
- Up to 3 cm: 50 + 40 = 90
- Up to 4 cm: 90 + 60 = 150
- Up to 5 cm: 150 + 50 = 200
- Up to 6 cm: 200 + 30 = 230
- Up to 7 cm: 230 + 20 = 250
- Up to 8 cm: 250 + 6 = 256
The cumulative frequencies show that the 128th and 129th seedlings fall within the 3 to 4 cm height bin.
Determine the Exact Median Using Linear Interpolation To estimate the median height within the 3-4 cm bin, apply linear interpolation.

The frequency that corresponds to the 3-4 cm height is 60. The cumulative frequency at the lower end (3 cm) is 90 and at the upper end (4 cm) is 150. Find the proportion of the seedlings within that height.

The formula for linear interpolation is:

$$ \text{Height} = L + \left( \frac{(N/2 - F)}{f} \right) \cdot w $$

Where:
- (L) = lower class boundary = 3 cm
- (N) = total number of seedlings = 256
- (F) = cumulative frequency before the class = 90
- (f) = frequency of the median class = 60
- (w) = width of the class = 1 cm (4 cm - 3 cm)
Substitute into the formula:

$$ \text{Height} = 3 + \left( \frac{(128 - 90)}{60} \right) \cdot 1 $$

$$ \text{Height} = 3 + \left( \frac{38}{60} \right) $$

$$ \text{Height} = 3 + 0.6333 \approx 3.63 \text{ cm} $$

The estimated median height of the seedlings is approximately $3.63$ cm.

More Information

The median is a useful statistic that represents the midpoint of a data set. In this case, estimating the median height is important for understanding the overall growth trends in the seedlings.

Tips

Confusing the mode for the median: Remember the median is the middle value, not the most frequent one.
Miscalculating cumulative frequencies: Double-check the sums as they determine where the median lies within the bins.