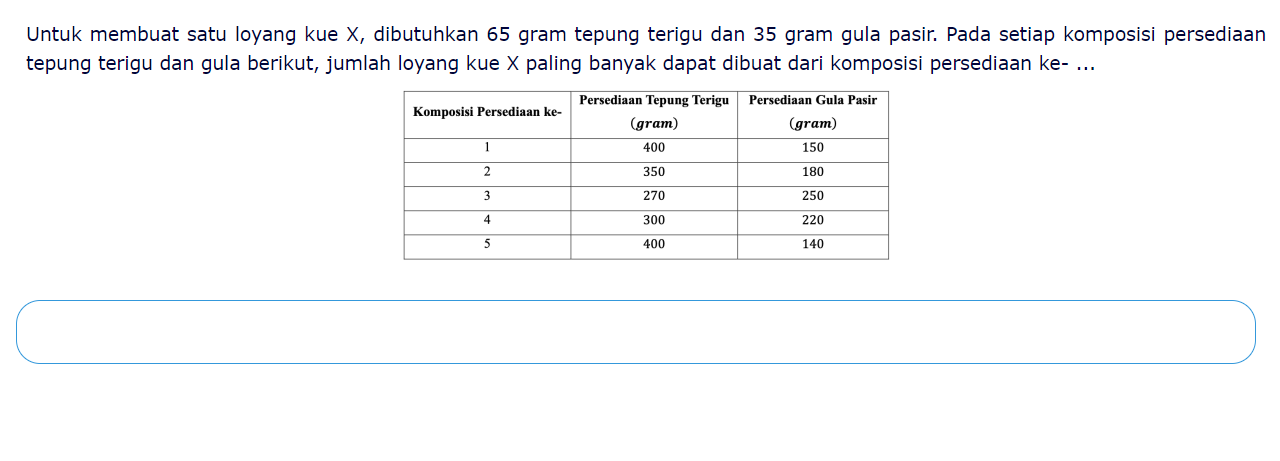
Untuk membuat satu loyang kue X, dibutuhkan 65 gram tepung terigu dan 35 gram gula pasir. Pada setiap komposisi persediaan tepung terigu dan gula pasir berikut, jumlah loyang kue X... Untuk membuat satu loyang kue X, dibutuhkan 65 gram tepung terigu dan 35 gram gula pasir. Pada setiap komposisi persediaan tepung terigu dan gula pasir berikut, jumlah loyang kue X paling banyak dapat dibuat dari komposisi persediaan ke- ... Read more

Steps to Solve

1. Identifikasi Kebutuhan untuk Satu Loyang Kue Untuk membuat satu loyang kue X, kita memerlukan 65 gram tepung terigu dan 35 gram gula pasir.

2. Hitung Jumlah Loyang dari Setiap Persediaan Kita akan menghitung jumlah loyang kue yang dapat dibuat berdasarkan setiap komposisi persediaan dengan rumus:

   $$ \text{Jumlah Loyang} = \frac{\text{Persediaan}}{\text{Kebutuhan per Loyang}} $$

   Hitung untuk setiap komposisi:

   • Komposisi 1:
     • Tepung Terigu: $$ \text{Jumlah Loyang} = \frac{400}{65} \approx 6.15 \quad \text{(dibulatkan ke 6)} $$
     • Gula Pasir: $$ \text{Jumlah Loyang} = \frac{150}{35} \approx 4.29 \quad \text{(dibulatkan ke 4)} $$
     • Minimum = 4
   • Komposisi 2:
     • Tepung Terigu: $$ \text{Jumlah Loyang} = \frac{350}{65} \approx 5.38 \quad \text{(dibulatkan ke 5)} $$
     • Gula Pasir: $$ \text{Jumlah Loyang} = \frac{180}{35} \approx 5.14 \quad \text{(dibulatkan ke 5)} $$
     • Minimum = 5
   • Komposisi 3:
     • Tepung Terigu: $$ \text{Jumlah Loyang} = \frac{270}{65} \approx 4.15 \quad \text{(dibulatkan ke 4)} $$
     • Gula Pasir: $$ \text{Jumlah Loyang} = \frac{250}{35} \approx 7.14 \quad \text{(dibulatkan ke 7)} $$
     • Minimum = 4
   • Komposisi 4:
     • Tepung Terigu: $$ \text{Jumlah Loyang} = \frac{300}{65} \approx 4.62 \quad \text{(dibulatkan ke 4)} $$
     • Gula Pasir: $$ \text{Jumlah Loyang} = \frac{220}{35} \approx 6.29 \quad \text{(dibulatkan ke 6)} $$
     • Minimum = 4
   • Komposisi 5:
     • Tepung Terigu: $$ \text{Jumlah Loyang} = \frac{400}{65} \approx 6.15 \quad \text{(dibulatkan ke 6)} $$
     • Gula Pasir: $$ \text{Jumlah Loyang} = \frac{140}{35} \approx 4.00 \quad \text{(dibulatkan ke 4)} $$
     • Minimum = 4

3. Kesimpulan Jumlah Loyang Kue dari Setiap Komposisi Sekarang, kita bisa menyusun jumlah loyang yang bisa dibuat dari masing-masing komposisi:

   • Komposisi 1: 4 loyang
   • Komposisi 2: 5 loyang
   • Komposisi 3: 4 loyang
   • Komposisi 4: 4 loyang
   • Komposisi 5: 4 loyang

4. Tentukan Komposisi dengan Jumlah Loyang Terbanyak Dari perhitungan di atas, komposisi yang dapat menghasilkan loyang terbanyak adalah komposisi ke-2.