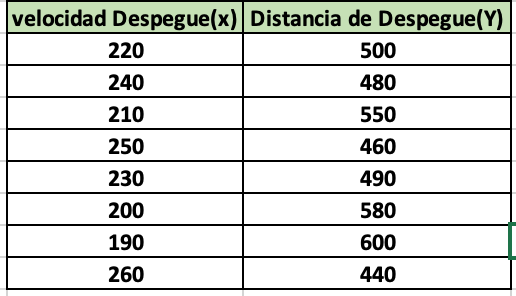
Un ingeniero aeronáutico está analizando la relación entre la velocidad de despegue de aviones y la distancia de despegue requerida. Se recopilaron datos de 10 vuelos de prueba y s... Un ingeniero aeronáutico está analizando la relación entre la velocidad de despegue de aviones y la distancia de despegue requerida. Se recopilaron datos de 10 vuelos de prueba y se registraron la velocidad de despegue (en km/h) y la distancia de despegue (en metros). ¿Cuál es el coeficiente de correlación? Estima la distancia de despegue para un avión que despega a una velocidad de 255 km/h. Read more

Steps to Solve

1. Calcular el coeficiente de correlación

Utilizaremos la fórmula del coeficiente de correlación de Pearson, que es:

$$ r = \frac{n(\sum{xy}) - (\sum{x})(\sum{y})}{\sqrt{[n\sum{x^2} - (\sum{x})^2][n\sum{y^2} - (\sum{y})^2]}} $$

Donde:

• $n$ es el número de pares de datos,
• $x$ son las velocidades de despegue,
• $y$ son las distancias de despegue.

Primero, calculamos las sumas necesarias:

• $n = 8$ (número de datos)
• Sumas:
  • $\sum{x} = 220 + 240 + 210 + 250 + 230 + 200 + 190 + 260 = 1880$
  • $\sum{y} = 500 + 480 + 550 + 460 + 490 + 580 + 600 + 440 = 4160$
  • $\sum{xy} = (220 \cdot 500) + (240 \cdot 480) + (210 \cdot 550) + (250 \cdot 460) + (230 \cdot 490) + (200 \cdot 580) + (190 \cdot 600) + (260 \cdot 440) = 106000 + 115200 + 115500 + 115000 + 112700 + 116000 + 114000 + 114400 = 872800$
  • $\sum{x^2} = 220^2 + 240^2 + 210^2 + 250^2 + 230^2 + 200^2 + 190^2 + 260^2 = 48400 + 57600 + 44100 + 62500 + 52900 + 40000 + 36100 + 67600 = 271200$
  • $\sum{y^2} = 500^2 + 480^2 + 550^2 + 460^2 + 490^2 + 580^2 + 600^2 + 440^2 = 250000 + 230400 + 302500 + 211600 + 240100 + 336400 + 360000 + 193600 = 1923600$

2. Calcular el coeficiente de correlación

Reemplazamos las sumas en la fórmula de $r$:

$$ r = \frac{8(872800) - (1880)(4160)}{\sqrt{[8(271200) - (1880)^2][8(1923600) - (4160)^2]}} $$

Ahora computamos estos productos y sumas:

• Numerador: $8 \cdot 872800 - 1880 \cdot 4160 = 6982400 - 7820800 = -838400$
• Denominador:
  • Para $x$: $8 \cdot 271200 - 1880^2 = 2169600 - 3534400 = -1364800$
  • Para $y$: $8 \cdot 1923600 - 4160^2 = 15388800 - 17305600 = -1907200$

Entonces tenemos:

$$ r = \frac{-838400}{\sqrt{(-1364800)(-1907200)}} $$

3. Sustitución y cálculo final

Calculamos:

$$ \sqrt{(-1364800)(-1907200)} = \sqrt{2605880320000} \approx 1613062.92 $$

Por lo tanto:

$$ r = \frac{-838400}{1613062.92} \approx -0.519 $$

4. Estimar la distancia de despegue para 255 km/h

Usaremos la regresión lineal, que se puede expresar como:

$$ Y = mX + b $$

Donde $m$ (pendiente) y $b$ (intersección) se calculan como:

$$ m = \frac{n(\sum{xy}) - (\sum{x})(\sum{y})}{n\sum{x^2} - (\sum{x})^2} $$ $$ b = \frac{\sum{y} - m\sum{x}}{n} $$

Utilizamos los valores calculados previamente para obtener $m$ y $b$ y luego sustituimos $X = 255$ para encontrar $Y$.

5. Sustitución para $m$ y $b$ y calcular

Finalmente, calculamos:

• m,
• b,
• Y cuando $X = 255$.