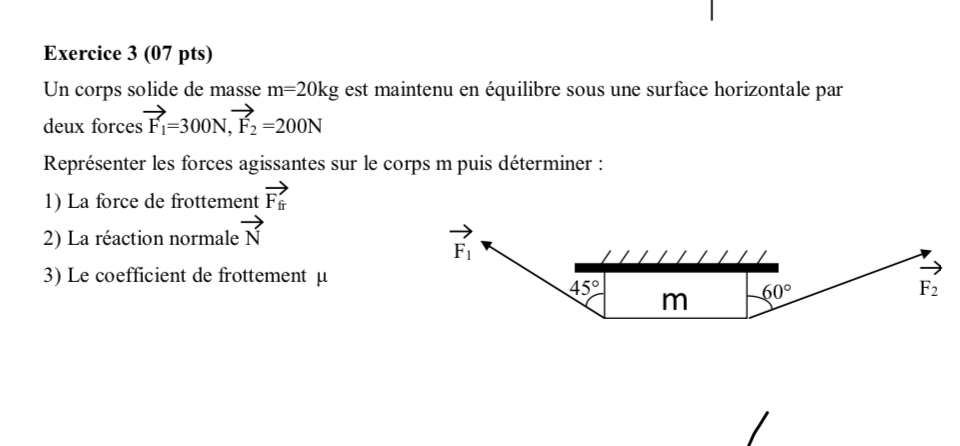
Un corps solide de masse m=20kg est maintenu en équilibre sous une surface horizontale par deux forces F1=300N, F2=200N. Représenter les forces agissantes sur le corps m puis déter... Un corps solide de masse m=20kg est maintenu en équilibre sous une surface horizontale par deux forces F1=300N, F2=200N. Représenter les forces agissantes sur le corps m puis déterminer : 1) La force de frottement Fr 2) La réaction normale N 3) Le coefficient de frottement μ.
Understand the Problem
La question demande de déterminer les forces agir sur un corps solide en équilibre sous une surface horizontale, donné des forces appliquées et une masse du corps. Il s'agit de représenter les forces et de calculer la force de frottement, la réaction normale, et le coefficient de frottement.
Answer
1) $F_r = 150\sqrt{2} - 100$ N, 2) $N = 196.2 - 150\sqrt{2} - 100\sqrt{3}$ N, 3) $\mu = \frac{150\sqrt{2} - 100}{196.2 - 150\sqrt{2} - 100\sqrt{3}}$.
Answer for screen readers
-
La force de frottement $F_r = 150\sqrt{2} - 100$ N.
-
La réaction normale $N = 196.2 - 150\sqrt{2} - 100\sqrt{3}$ N.
-
Le coefficient de frottement $\mu = \frac{150\sqrt{2} - 100}{196.2 - 150\sqrt{2} - 100\sqrt{3}}$.
Steps to Solve
-
Représentation des forces
Représentez les forces agissant sur le corps m. Les forces appliquées sont $F_1 = 300N$ à un angle de $45^\circ$ et $F_2 = 200N$ à un angle de $60^\circ$.
Les composantes de ces forces peuvent être décomposées comme suit :
-
Pour $F_1$ :
-
$F_{1x} = F_1 \cdot \cos(45^\circ) = 300 \cdot \frac{\sqrt{2}}{2} = 150\sqrt{2}$
-
$F_{1y} = F_1 \cdot \sin(45^\circ) = 300 \cdot \frac{\sqrt{2}}{2} = 150\sqrt{2}$
-
Pour $F_2$ :
-
$F_{2x} = F_2 \cdot \cos(60^\circ) = 200 \cdot \frac{1}{2} = 100$
-
$F_{2y} = F_2 \cdot \sin(60^\circ) = 200 \cdot \frac{\sqrt{3}}{2} = 100\sqrt{3}$
-
-
Calcul de la somme des forces dans la direction x
Puisque le corps est en équilibre, la somme des forces dans la direction x doit être nulle :
$$ F_{1x} - F_{2x} - F_r = 0 $$
On remplace par les valeurs calculées :
$$ 150\sqrt{2} - 100 - F_r = 0 $$
Ainsi, on peut isoler $F_r$ :
$$ F_r = 150\sqrt{2} - 100 $$
-
Calcul de la somme des forces dans la direction y
Pour la direction y, la réaction normale $N$ doit équilibrer les forces verticales :
$$ N - (mg) + F_{1y} + F_{2y} = 0 $$
Le poids $mg$ se calcule comme suit :
$$ mg = 20 \cdot 9.81 = 196.2 , N $$
En insérant les composants :
$$ N - 196.2 + 150\sqrt{2} + 100\sqrt{3} = 0 $$
Ainsi, on peut résoudre pour $N$ :
$$ N = 196.2 - 150\sqrt{2} - 100\sqrt{3} $$
-
Calcul du coefficient de frottement μ
Enfin, le coefficient de frottement $\mu$ est donné par la relation :
$$ F_r = \mu N $$
On peut exprimer $\mu$ comme suit :
$$ \mu = \frac{F_r}{N} $$
En remplaçant $F_r$ et $N$ par leurs expressions calculées précédemment.
-
La force de frottement $F_r = 150\sqrt{2} - 100$ N.
-
La réaction normale $N = 196.2 - 150\sqrt{2} - 100\sqrt{3}$ N.
-
Le coefficient de frottement $\mu = \frac{150\sqrt{2} - 100}{196.2 - 150\sqrt{2} - 100\sqrt{3}}$.
More Information
Les force appliquées sont représentées par des vecteurs, et la décomposition en composantes permet de calculer le comportement du système en équilibre. Les forces de frottement et la réaction normale sont essentielles dans les problèmes d'équilibre statique.
Tips
- Ne pas décomposer correctement les forces en leurs composantes.
- Oublier le poids du corps dans la direction verticale.
- Erreurs dans l'application des formules d'équilibre (somme des forces = 0).
AI-generated content may contain errors. Please verify critical information