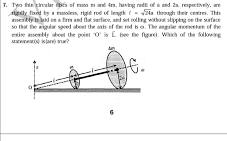
Two thin circular disks of mass m1 and m2, having radii r1 and r2 respectively, are slightly fixed by a massless, right rod of length L = r1 + r2 through their centers. This assemb... Two thin circular disks of mass m1 and m2, having radii r1 and r2 respectively, are slightly fixed by a massless, right rod of length L = r1 + r2 through their centers. This assembly is held in a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the point 'O' is L, see the figure. Which of the following statements is correct about the point 'O'?
Understand the Problem
The question is asking about the angular momentum of a system of cylindrical disks rotating about a point. It requires an understanding of rotational dynamics and how to calculate angular momentum.
Answer
The angular momentum about point \( O \) is given by \( L_O = \left( \frac{5}{2} m_1 r_1^2 + \frac{5}{2} m_2 r_2^2 \right) \omega \).
Answer for screen readers
The angular momentum about point ( O ) is given by: $$ L_O = \left( \frac{5}{2} m_1 r_1^2 + \frac{5}{2} m_2 r_2^2 \right) \omega $$
Steps to Solve
- Identify the System's Parameters
Let ( m_1 ) and ( m_2 ) be the masses of the disks, ( r_1 ) and ( r_2 ) be their respective radii, and ( L = r_1 + r_2 ).
- Formulate the Angular Momentum about Point O
The angular momentum ( L_O ) about point ( O ) is given by: $$ L_O = I_O \omega + r_{cm} \times mv $$ where ( I_O ) is the moment of inertia about point ( O ), ( v ) is the velocity of the center of mass, and ( \omega ) is the angular speed about ( O ).
- Calculate Moment of Inertia
The moment of inertia of a single disk about its center is: $$ I_{\text{disk}} = \frac{1}{2} m r^2 $$ For two disks, the total moment of inertia about point ( O ) (using the parallel axis theorem) is: $$ I_O = I_{1} + I_{2} + m_1 d_1^2 + m_2 d_2^2 $$ where ( d_1 = r_1 ) and ( d_2 = r_2 ).
- Use angular speed Value
Given ( \omega = \frac{L}{r_1 + r_2} ) and substituting into ( L_O ): $$ L_O = \left( \frac{1}{2} m_1 r_1^2 + \frac{1}{2} m_2 r_2^2 + m_1 r_1^2 + m_2 r_2^2 \right) \omega $$
- Result Interpretation
Analyze the resulting equation to determine characteristics about point ( O ) compared to other points in the system.
The angular momentum about point ( O ) is given by: $$ L_O = \left( \frac{5}{2} m_1 r_1^2 + \frac{5}{2} m_2 r_2^2 \right) \omega $$
More Information
Angular momentum depends on the distribution of mass relative to the axis of rotation. The configuration of the disks affects the overall inertia and thereby the angular momentum.
Tips
- Miscalculating the moment of inertia when combining two or more objects.
- Forgetting to apply the parallel axis theorem when needed, leading to incorrect results for angular momentum.
AI-generated content may contain errors. Please verify critical information