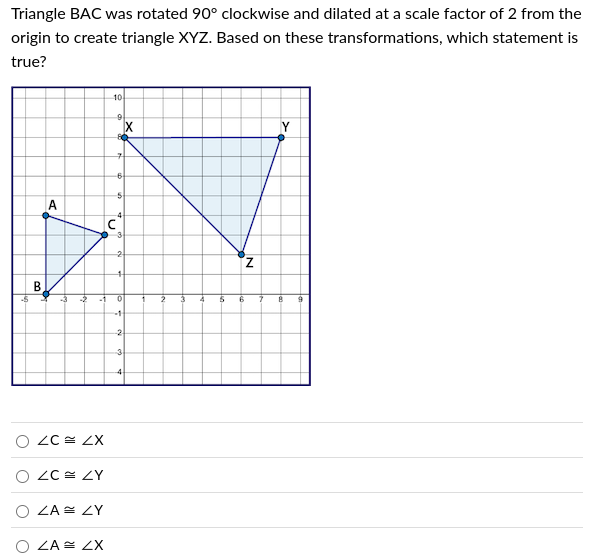
Triangle BAC was rotated 90° clockwise and dilated at a scale factor of 2 from the origin to create triangle XYZ. Based on these transformations, which statement is true?
Understand the Problem
The question is asking to determine which angle relationships are true after performing a rotation and dilation on triangle BAC to create triangle XYZ. This involves understanding geometric transformations and the properties of corresponding angles.
Answer
The true statement is \( \angle C \cong \angle X \).
Answer for screen readers
The true statement is ( \angle C \cong \angle X ).
Steps to Solve
-
Identify Transformation Effects The triangle BAC is first rotated 90° clockwise and then dilated by a scale factor of 2. A rotation preserves angle measures and the dilation preserves angle relationships but changes the size of the triangle.
-
Analyze Corresponding Angles Since transformations such as rotation and dilation do not alter angles, we need to check the corresponding angles in triangles BAC and XYZ. After rotation and dilation, the angles of BAC will correspond to angles in XYZ.
-
Determine Corresponding Angle Relationships
- The vertex ( B ) in triangle BAC corresponds to ( Z ) in triangle XYZ.
- The vertex ( A ) corresponds to vertex ( Y ).
- The vertex ( C ) corresponds to vertex ( X ).
This gives us the relations:
- ( \angle A ) corresponds to ( \angle Y )
- ( \angle B ) corresponds to ( \angle Z )
- ( \angle C ) corresponds to ( \angle X )
- Identify True Statements Based on the angle correspondence, we evaluate the options:
- ( \angle C \cong \angle X )
- ( \angle C \cong \angle Y )
- ( \angle A \cong \angle Y )
- ( \angle A \cong \angle X )
From the observations, we find that ( \angle C \cong \angle X ) is true.
The true statement is ( \angle C \cong \angle X ).
More Information
This question revolves around the properties of geometric transformations, specifically how angle measures are preserved through rotations and dilations. Understanding these transformations helps determine corresponding angles in transformed shapes.
Tips
- Confusing angle correspondence after transformations. It’s essential to track which vertex corresponds to which after shifting the triangle.
- Not remembering that angle measures remain the same under rotation and dilation.
AI-generated content may contain errors. Please verify critical information