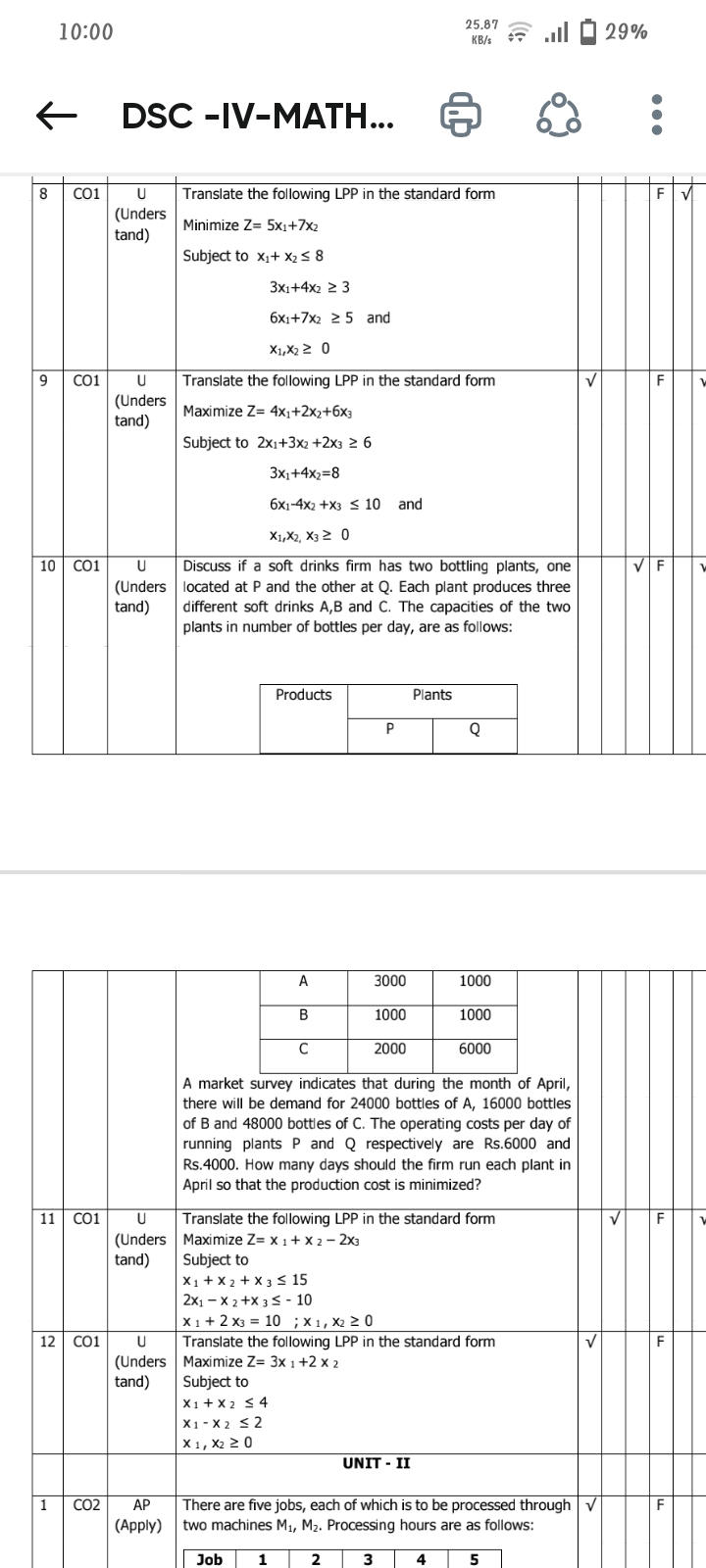
Translate the following LPP in the standard form Minimize Z = 5x1 + 7x2 Subject to x1 + x2 ≤ 8, 3x1 + 4x2 ≥ 3, 6x1 + 7x2 ≥ 5 and x1, x2 ≥ 0.

Steps to Solve

1. Standard Form for Minimization Problem

For the first linear programming problem, we need to translate it into standard form. Standard form for a minimization problem requires all constraints to be in the form of equalities.

• Objective function: $$ Z = 5x_1 + 7x_2 $$

2. Convert Inequalities to Equalities

We need to convert the inequalities into equations by adding slack or surplus variables.

• Constraints:

1. From the constraint ( x_1 + x_2 \leq 8 ):

   • Introduce slack variable ( s_1 ): $$ x_1 + x_2 + s_1 = 8 $$

2. From the constraint ( 3x_1 + 4x_2 \geq 3 ):

   • Introduce surplus variable ( s_2 ): $$ 3x_1 + 4x_2 - s_2 = 3 $$

3. From the constraint ( 6x_1 + 7x_2 \geq 5 ):

   • Introduce surplus variable ( s_3 ): $$ 6x_1 + 7x_2 - s_3 = 5 $$

3. Non-negativity Constraints

The requirements ( x_1, x_2 \geq 0 ) remain the same. It also applies to the added slack and surplus variables ( s_1, s_2, s_3 \geq 0 ).

4. Final Standard Form

Thus, the complete standard form for this LPP is:

• Objective Function: $$ \text{Minimize } Z = 5x_1 + 7x_2 $$

• Subject to:

1. $$ x_1 + x_2 + s_1 = 8 $$
2. $$ 3x_1 + 4x_2 - s_2 = 3 $$
3. $$ 6x_1 + 7x_2 - s_3 = 5 $$
4. $$ x_1, x_2, s_1, s_2, s_3 \geq 0 $$

5. Translate Second LPP to Standard Form

For the second linear programming problem, we similarly need to rewrite it for maximization.

• Objective function: $$ Z = 4x_1 + 2x_2 + 6x_3 $$

6. Convert Inequalities to Equalities

• Constraints:

1. From ( 2x_1 + 3x_2 + 2x_3 \geq 6 ):

   • Introduce surplus variable ( s_1 ): $$ 2x_1 + 3x_2 + 2x_3 - s_1 = 6 $$

2. From ( 3x_1 + 4x_2 = 8 ):

   • This already fits an equality form.

3. From ( 6x_1 - 4x_2 + x_3 \leq 10 ):

   • Introduce slack variable ( s_2 ): $$ 6x_1 - 4x_2 + x_3 + s_2 = 10 $$