Tracer la courbe de la cinétique plasmatique sur un papier semi-logarithmique. Commenter la courbe cinétique puis donner l’équation adéquate. Procéder à l’analyse mathématique de l... Tracer la courbe de la cinétique plasmatique sur un papier semi-logarithmique. Commenter la courbe cinétique puis donner l’équation adéquate. Procéder à l’analyse mathématique de la courbe. Déterminer les constantes de vitesse. Déterminer le temps de demi-vie d’élimination. Calculer la surface sous la courbe. Calculer la clairance et le volume de distribution. Interpréter la valeur de ce volume de distribution.
Understand the Problem
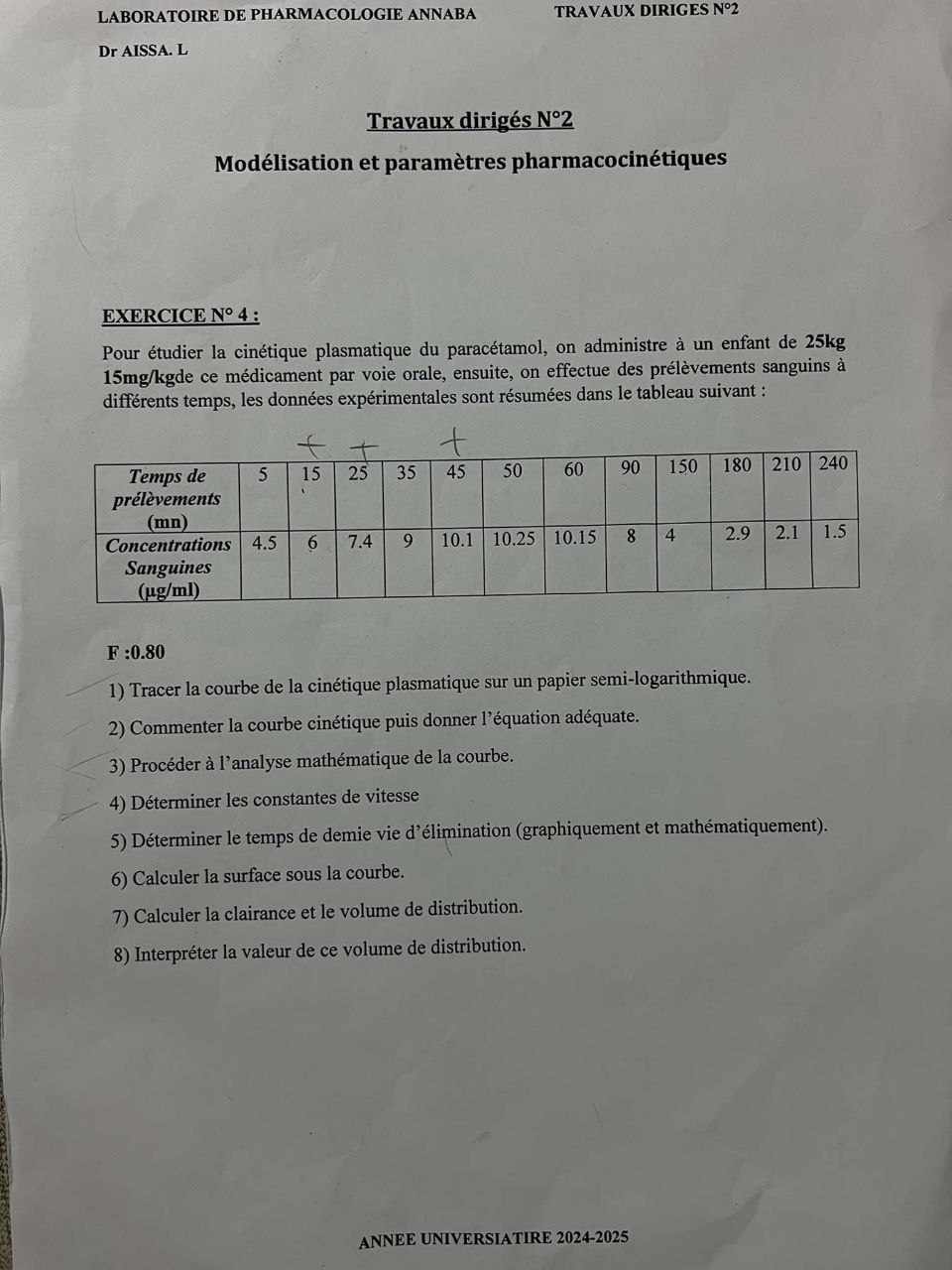
La question demande d'analyser la cinétique plasmatique du paracétamol administré à un enfant à partir de données expérimentales. Il s'agit de tracer la courbe, commenter, analyser mathématiquement, et calculer divers paramètres pharmacocinétiques comme les constantes de vitesse et le volume de distribution.
Answer
Le modèle cinétique du paracétamol suit une forme exponentielle décroissante, avec des constantes de vitesse et des calculs de clairance selon les équations correspondantes.
Answer for screen readers
Les résultats finaux des différents paramètres pharmacocinétiques seront basés sur les calculs de chaque étape ci-dessus.
Steps to Solve
- Tracer la courbe sur papier semi-logarithmique
Commencez par mettre les temps en abscisse (axe x) et les concentrations en ordonnée (axe y) sur du papier semi-logarithmique. Les données sont :
- Temps (mn) : 5, 15, 25, 35, 45, 50, 60, 90, 150, 180, 210, 240
- Concentrations (µg/ml) : 4.5, 6.7, 7.4, 10.1, 10.25, 10.15, 8, 2.9, 2.1, 1.5
- Commenter la courbe et donner l'équation adéquate
Analysez le tracé pour déterminer si la relation entre le temps et la concentration suit un modèle exponentiel décroissant. Dans ce cas, l'équation de la courbe peut être exprimée comme : $$ C(t) = C_0 e^{-kt} $$ où $C_0$ est la concentration initiale et $k$ est la constante de dégradation.
- Analyse mathématique de la courbe
Appliquez la transformation logarithmique pour linéariser la relation. Prenez le logarithme naturel des concentrations : $$ \ln(C) = \ln(C_0) - kt $$
- Déterminer les constantes de vitesse
À partir de la pente de la droite obtenue par la transformation logarithmique, vous pouvez déterminer la constante de vitesse $k$. Cela se fait en calculant la pente de la droite :
$$ k = -\frac{\Delta \ln(C)}{\Delta t} $$
- Déterminer le temps de demi-vie d'élimination
Le temps de demi-vie $t_{1/2}$ est donné par : $$ t_{1/2} = \frac{\ln(2)}{k} $$
- Calculer la surface sous la courbe
Utilisez des méthodes d'intégration (comme la méthode trapézoïdale) pour estimer la surface sous la courbe, qui représente l'exposition au médicament.
- Calculer la clairance et le volume de distribution
La clairance (CL) et le volume de distribution (Vd) sont calculés respectivement par les formules : $$ CL = \frac{Dose}{AUC} $$ $$ V_d = \frac{Dose}{C_0} $$
- Interpréter la valeur du volume de distribution
Après avoir calculé le volume de distribution, interprétez son impact sur l'efficacité et la sécurité du médicament en fonction des valeurs attendues pour d'autres médicaments similaires.
Les résultats finaux des différents paramètres pharmacocinétiques seront basés sur les calculs de chaque étape ci-dessus.
More Information
La pharmacocinétique étudie le mouvement des médicaments dans l'organisme et aide à établir des schémas posologiques adéquats.
Tips
- Oublier de transformer les concentrations en logarithmes lors de l'analyse de la courbe.
- Ne pas prendre en compte l'unité de mesure lors du calcul des constantes de vitesse et des volumes.
AI-generated content may contain errors. Please verify critical information