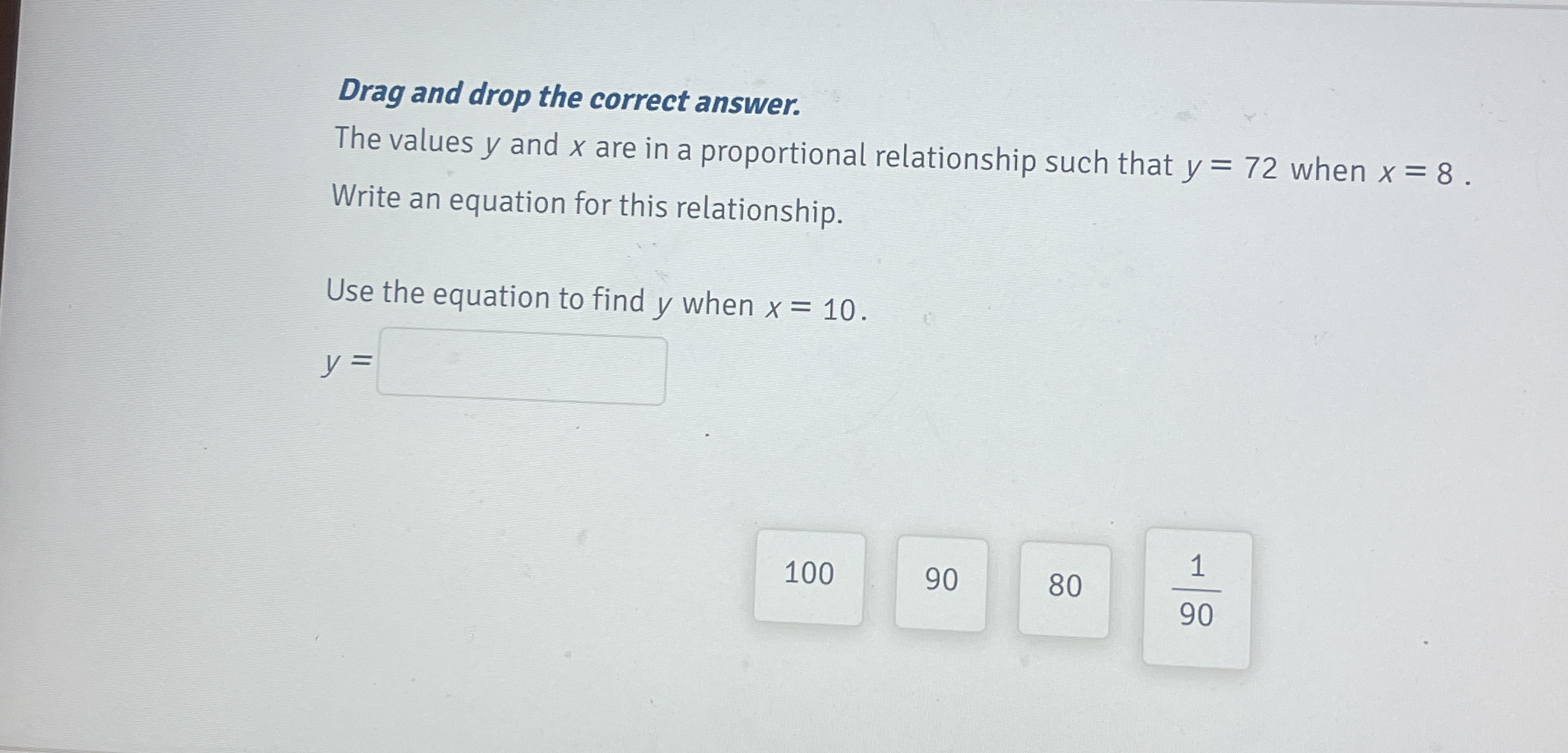
The values y and x are in a proportional relationship such that y = 72 when x = 8. Write an equation for this relationship. Use the equation to find y when x = 10.
Understand the Problem
The question is asking to establish a proportional relationship between the values of x and y, based on the provided values (y = 72 when x = 8). Then, we need to derive an equation representing this relationship and use it to calculate the value of y when x = 10.
Answer
$y = 90$
Answer for screen readers
The value of $y$ when $x = 10$ is $90$.
Steps to Solve
- Establish Proportional Relationship
Since $y$ is directly proportional to $x$, we can express this relationship as:
$$ y = kx $$
where $k$ is the constant of proportionality.
- Find the Constant of Proportionality
We know that $y = 72$ when $x = 8$. Using this information, we can substitute these values into the equation to find $k$:
$$ 72 = k \cdot 8 $$
To find $k$, divide both sides by 8:
$$ k = \frac{72}{8} = 9 $$
- Write the Equation
Now that we have $k$, we can write the full equation representing the relationship between $y$ and $x$:
$$ y = 9x $$
- Calculate $y$ when $x = 10$
To find $y$ when $x = 10$, substitute $10$ into the equation:
$$ y = 9 \cdot 10 = 90 $$
The value of $y$ when $x = 10$ is $90$.
More Information
The relationship established indicates that for every unit increase in $x$, $y$ increases by 9. This type of relationship is common in proportional reasoning and can be applied to various real-life situations.
Tips
- Forgetting to express the proportional relationship correctly as $y = kx$.
- Miscalculating $k$ by neglecting to divide correctly.
- Failing to substitute the value of $x$ correctly into the final equation for $y$.
AI-generated content may contain errors. Please verify critical information