The total number of values of x for which {x} = x (where {} denotes the fractional part function) is
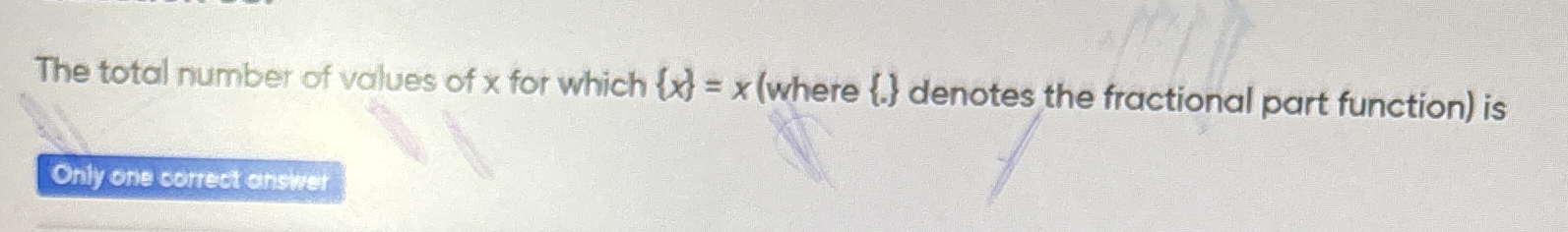
Understand the Problem
The question is asking for the total number of values of x that satisfy the equation involving the fractional part function, denoted by curly braces. This requires understanding the properties of the fractional part function to find the solutions.
Answer
Infinite
Answer for screen readers
The total number of values of $x$ that satisfy the equation is infinite.
Steps to Solve
- Understanding the Fractional Part Function
The fractional part function, denoted as ${x}$, is defined as ${x} = x - \lfloor x \rfloor$. This means it represents the "decimal" part of $x$.
- Setting Up the Equation
We need to solve the equation ${x} = x$. Substituting the definition of the fractional part, we write:
$$ x - \lfloor x \rfloor = x $$
- Simplifying the Equation
Rearranging the equation gives:
$$ -\lfloor x \rfloor = 0 $$
This implies that:
$$ \lfloor x \rfloor = 0 $$
- Interpreting the Floor Function Result
The floor function $\lfloor x \rfloor = 0$ means that $x$ must be in the interval:
$$ 0 \leq x < 1 $$
- Counting the Total Values
Since $x$ can take any real value from 0 up to, but not including, 1, there are infinitely many values of $x$ in the interval $[0, 1)$.
The total number of values of $x$ that satisfy the equation is infinite.
More Information
This result stems from the fact that the fractional part function can yield non-integer values in the interval from 0 to 1, revealing an infinite set of solutions.
Tips
null
AI-generated content may contain errors. Please verify critical information