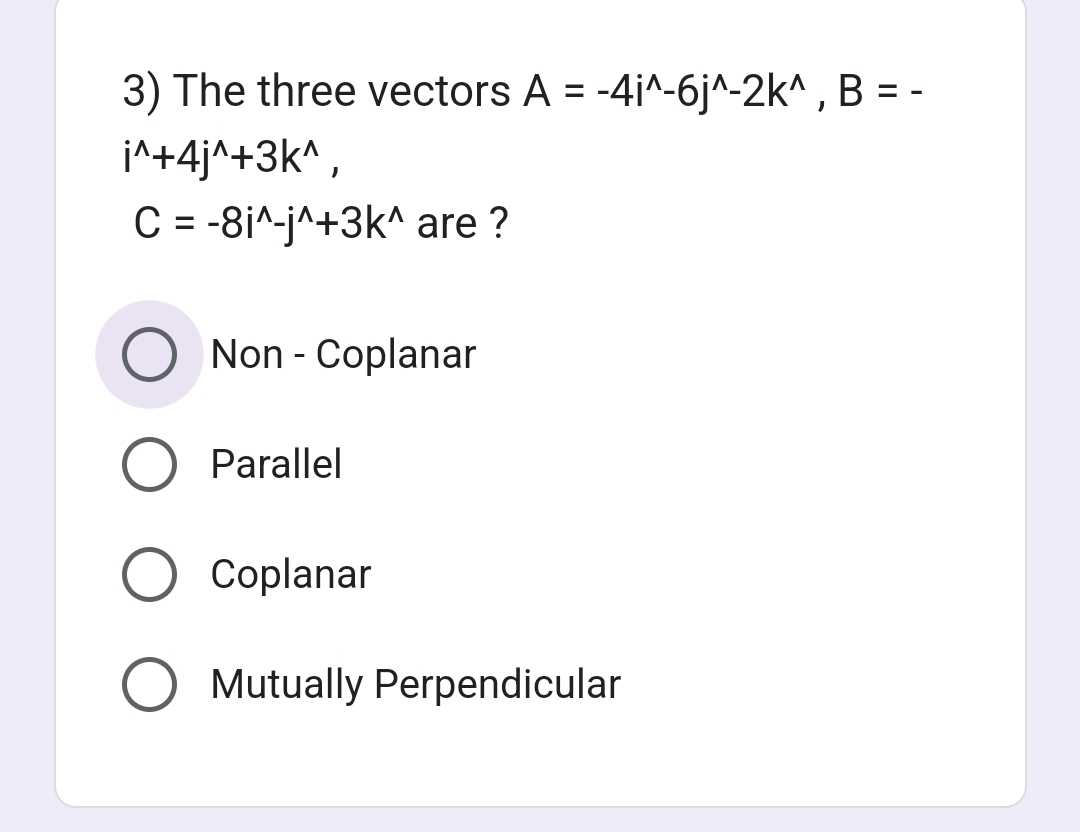
The three vectors A = -4i^-6j^-2k^, B = -i+4j+3k, C = -8i-j+3k are?
Understand the Problem
The question asks about the relationship between three given vectors A, B, and C, specifically whether they are non-coplanar, parallel, coplanar, or mutually perpendicular. To answer, we need to analyze the vectors' properties in three-dimensional space.
Answer
The vectors are coplanar.
Answer for screen readers
The three vectors ( \mathbf{A} ), ( \mathbf{B} ), and ( \mathbf{C} ) are Coplanar.
Steps to Solve
- List the Vectors
The given vectors are:
- ( \mathbf{A} = -4\mathbf{i} - 6\mathbf{j} - 2\mathbf{k} )
- ( \mathbf{B} = -\mathbf{i} + 4\mathbf{j} + 3\mathbf{k} )
- ( \mathbf{C} = -8\mathbf{i} - \mathbf{j} + 3\mathbf{k} )
- Form a Matrix
Construct a matrix using the components of the vectors ( \mathbf{A} ), ( \mathbf{B} ), and ( \mathbf{C} ): $$ \begin{bmatrix} -4 & -6 & -2 \ -1 & 4 & 3 \ -8 & -1 & 3 \end{bmatrix} $$
- Calculate the Determinant
Calculate the determinant of the matrix to determine whether the vectors are coplanar: $$ \text{det} = -4 \begin{vmatrix} 4 & 3 \ -1 & 3 \end{vmatrix} - (-6) \begin{vmatrix} -1 & 3 \ -8 & 3 \end{vmatrix} - 2 \begin{vmatrix} -1 & 4 \ -8 & -1 \end{vmatrix} $$
- Compute Individual 2x2 Determinants
Calculate each of the 2x2 determinants:
- For ( \begin{vmatrix} 4 & 3 \ -1 & 3 \end{vmatrix} = (4 \cdot 3) - (3 \cdot -1) = 12 + 3 = 15 )
- For ( \begin{vmatrix} -1 & 3 \ -8 & 3 \end{vmatrix} = (-1 \cdot 3) - (3 \cdot -8) = -3 + 24 = 21 )
- For ( \begin{vmatrix} -1 & 4 \ -8 & -1 \end{vmatrix} = (-1 \cdot -1) - (4 \cdot -8) = 1 + 32 = 33 )
- Substitute Back into Determinant Equation
Substituting back into the determinant formula: $$ \text{det} = -4(15) + 6(21) - 2(33) = -60 + 126 - 66 = 0 $$
- Interpret the Result
The determinant is zero, which indicates that the vectors ( \mathbf{A} ), ( \mathbf{B} ), and ( \mathbf{C} ) are coplanar.
The three vectors ( \mathbf{A} ), ( \mathbf{B} ), and ( \mathbf{C} ) are Coplanar.
More Information
Vectors are coplanar when they lie on the same plane in three-dimensional space. This is determined by the condition that the determinant of the matrix formed by their components is zero.
Tips
- Not forming the correct matrix of vector components.
- Failing to correctly calculate the determinants of the 2x2 matrices.
- Misinterpreting the result of the determinant (remember, a determinant of zero means coplanarity).
AI-generated content may contain errors. Please verify critical information