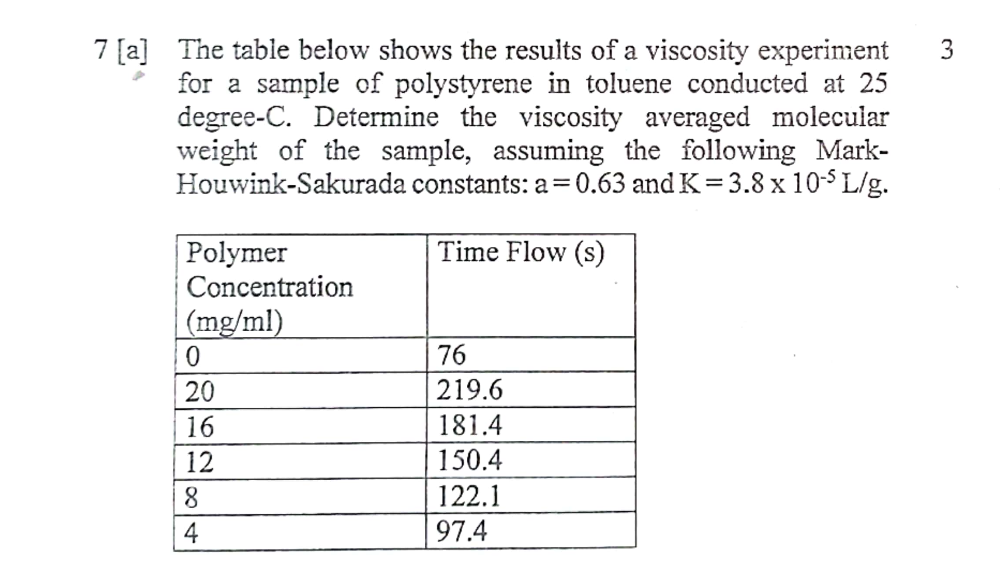
The table below shows the results of a viscosity experiment for a sample of polystyrene in toluene conducted at 25 degree-C. Determine the viscosity averaged molecular weight of th... The table below shows the results of a viscosity experiment for a sample of polystyrene in toluene conducted at 25 degree-C. Determine the viscosity averaged molecular weight of the sample, assuming the following Mark-Houwink-Sakurada constants: a = 0.63 and K = 3.8 x 10^-5 L/g. Read more

Steps to Solve

1. Calculate the reduced viscosity

Reduced viscosity (([\eta]_r)) is given by:

$$ [\eta]_r = \frac{(t-t_0)}{c} $$

where:

• ( t ) = time flow for the polymer solution
• ( t_0 ) = time flow for the solvent (0 mg/ml concentration)
• ( c ) = concentration in g/ml.

For each concentration, calculate ([\eta]_r):

• For 20 mg/ml: ( c = 0.02 ) g/ml
• For 16 mg/ml: ( c = 0.016 ) g/ml
• For 12 mg/ml: ( c = 0.012 ) g/ml
• For 8 mg/ml: ( c = 0.008 ) g/ml
• For 4 mg/ml: ( c = 0.004 ) g/ml

2. Calculate the intrinsic viscosity

Intrinsic viscosity (([\eta])) is calculated by taking the limit of reduced viscosity as concentration approaches zero. You can plot reduced viscosity against concentration and fit a line or use the values for calculation:

• ([\eta] = \lim_{c \to 0} [\eta]_r)

3. Apply the Mark-Houwink relation

We can use the Mark-Houwink equation to find the viscosity averaged molecular weight ((M)):

$$ [\eta] = K M^a $$

Rearranging gives:

$$ M = \left(\frac{[\eta]}{K}\right)^{\frac{1}{a}} $$

4. Input values into the equation

Once we compute ([\eta]), we can substitute (K = 3.8 \times 10^{-5}) L/g and (a = 0.63) into the equation to solve for (M).