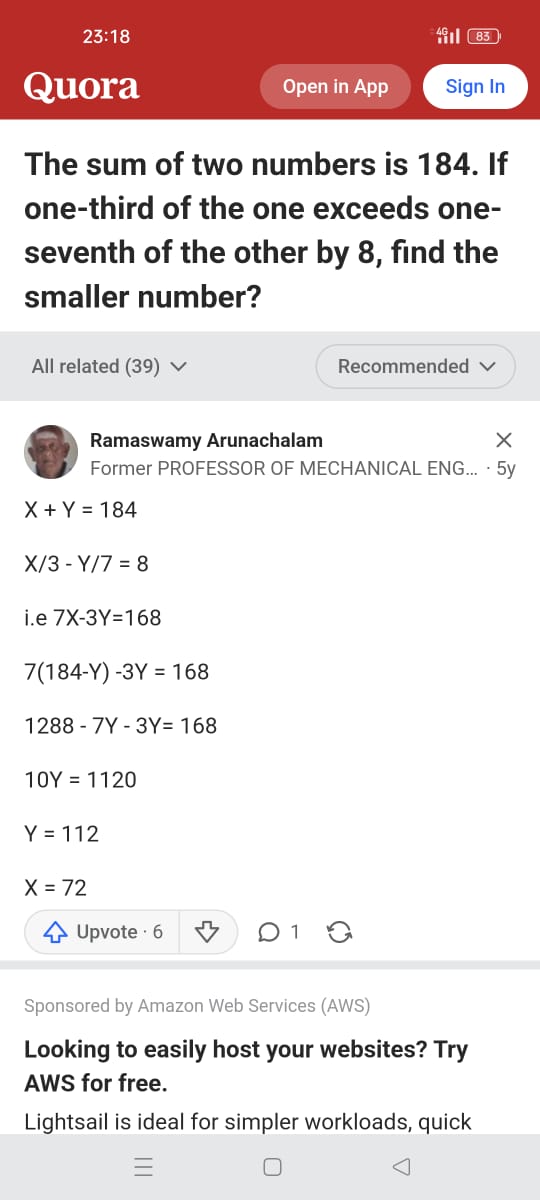
The sum of two numbers is 184. If one-third of one exceeds one-seventh of the other by 8, find the smaller number?

Steps to Solve

1. Define Variables
   Let ( X ) be the first number and ( Y ) be the second number.

2. Set Up the First Equation
   From the problem statement, we know that the sum of the two numbers is 184:
   $$ X + Y = 184 $$

3. Set Up the Second Equation
   According to the condition that one-third of one number exceeds one-seventh of the other number by 8, we can write:
   $$ \frac{X}{3} - \frac{Y}{7} = 8 $$

4. Eliminate Fractions
   Multiply the entire second equation by 21 (which is the least common multiple of 3 and 7) to eliminate the fractions:
   $$ 21 \left(\frac{X}{3}\right) - 21 \left(\frac{Y}{7}\right) = 21 \cdot 8 $$
   This simplifies to:
   $$ 7X - 3Y = 168 $$

5. Substitute for One Variable
   Solve the first equation for ( Y ):
   $$ Y = 184 - X $$

6. Substitute into the Second Equation
   Now substitute ( Y ) in the second equation:
   $$ 7X - 3(184 - X) = 168 $$

7. Simplify the Equation
   Distributing the -3 gives:
   $$ 7X - 552 + 3X = 168 $$
   Combine like terms:
   $$ 10X - 552 = 168 $$

8. Solve for ( X )
   Add 552 to both sides:
   $$ 10X = 720 $$
   Now divide by 10:
   $$ X = 72 $$

9. Find ( Y )
   Using ( Y = 184 - X ):
   $$ Y = 184 - 72 = 112 $$