The sets A = {x: x is an odd number}, B = {x: x is a factor of 60} and C = {x: x is a prime number} are the subsets of U = {x: x is a natural number and x < 9}. Find: (a) A ∩ B (b)... The sets A = {x: x is an odd number}, B = {x: x is a factor of 60} and C = {x: x is a prime number} are the subsets of U = {x: x is a natural number and x < 9}. Find: (a) A ∩ B (b) B' ∩ C (c) A ∩ B ∩ C (d) B ∪ C
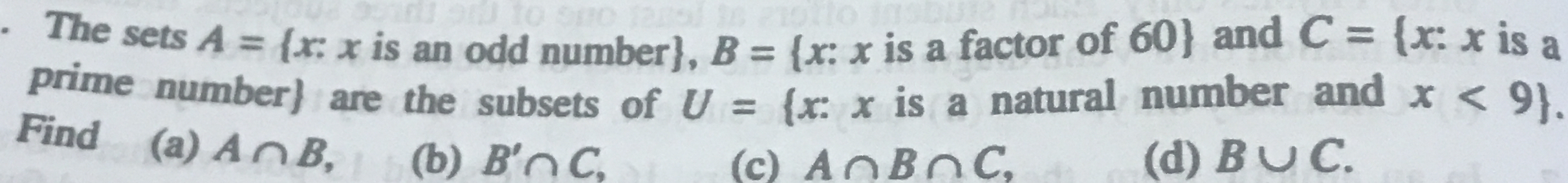
Understand the Problem
The question involves set theory. We have sets A, B, and C defined based on properties of their elements (odd numbers, factors of 60, and prime numbers, respectively). These sets are subsets of a universal set U, which consists of natural numbers less than 9. The task is to find the intersection and union of these sets (A ∩ B, B' ∩ C, A ∩ B ∩ C, and B ∪ C).
Answer
(a) $A \cap B = \{1, 3, 5\}$ (b) $B' \cap C = \{7\}$ (c) $A \cap B \cap C = \{3, 5\}$ (d) $B \cup C = \{1, 2, 3, 4, 5, 6, 7\}$
Answer for screen readers
(a) $A \cap B = {1, 3, 5}$ (b) $B' \cap C = {7}$ (c) $A \cap B \cap C = {3, 5}$ (d) $B \cup C = {1, 2, 3, 4, 5, 6, 7}$
Steps to Solve
- Define the universal set $U$
$U$ is the set of natural numbers less than 9, so $U = {1, 2, 3, 4, 5, 6, 7, 8}$.
- Define set $A$
Set $A$ consists of odd numbers in $U$, so $A = {1, 3, 5, 7}$.
- Define set $B$
Set $B$ consists of factors of 60 in $U$. The factors of 60 are 1, 2, 3, 4, 5, 6, so $B = {1, 2, 3, 4, 5, 6}$.
- Define set $C$
Set $C$ consists of prime numbers in $U$, so $C = {2, 3, 5, 7}$.
- Find $A \cap B$
$A \cap B$ is the intersection of sets $A$ and $B$, containing elements that are in both $A$ and $B$. Thus, $A \cap B = {1, 3, 5}$.
- Find $B'$ (the complement of $B$ in $U$)
The complement of $B$ consists of elements in $U$ that are not in $B$. So, $B' = {7, 8}$.
- Find $B' \cap C$
$B' \cap C$ is the intersection of sets $B'$ and $C$, containing elements that are in both $B'$ and $C$. Thus, $B' \cap C = {7}$.
- Find $A \cap B \cap C$
$A \cap B \cap C$ is the intersection of sets $A$, $B$, and $C$, meaning the elements that are in all three sets. $A \cap B = {1, 3, 5}$. $(A \cap B) \cap C = {3, 5}$. Thus, $A \cap B \cap C = {3, 5}$.
- Find $B \cup C$
$B \cup C$ is the union of sets $B$ and $C$, containing all elements that are in $B$ or $C$ or both. Thus, $B \cup C = {1, 2, 3, 4, 5, 6, 7}$.
(a) $A \cap B = {1, 3, 5}$ (b) $B' \cap C = {7}$ (c) $A \cap B \cap C = {3, 5}$ (d) $B \cup C = {1, 2, 3, 4, 5, 6, 7}$
More Information
The intersection of two sets contains the elements common to both sets. The union of two sets combines the elements of both sets into one set, without repetition. The complement of a set contains the elements in the universal set that are not in given set. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves.
Tips
A common mistake is to forget to restrict the elements to the universal set $U$. For example, a factor of 60 is 10, but 10 is not in the universal set $U$, so it cannot be in set $B$. Also, students might make errors in identifying prime numbers or factors of 60. Another common mistake is in the definition of intersection and union, confusing the two.
AI-generated content may contain errors. Please verify critical information