The root of the function, f(x) = x³ - 2x² + 3x - 1 in the interval [0, 1] using bisection method after two iterations, is ______. (round off up to 2 decimals)
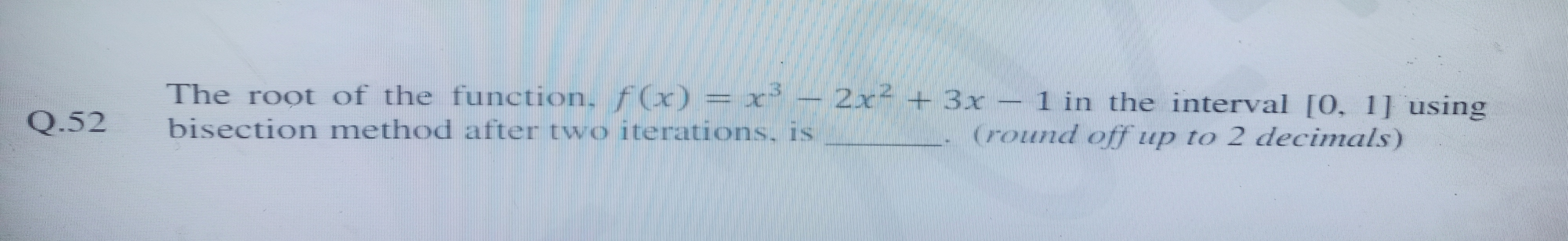
Understand the Problem
The question is asking to find the root of a cubic function using the bisection method, specifically after completing two iterations. The function given is f(x) = x³ - 2x² + 3x - 1 within the interval [0, 1], and the result should be rounded to two decimal places.
Answer
The root of the function after two iterations is approximately $0.25$.
Answer for screen readers
The root of the function after two iterations is approximately $0.25$.
Steps to Solve
-
Define the function and interval We have the function ( f(x) = x^3 - 2x^2 + 3x - 1 ) and the interval ([0, 1]).
-
Calculate initial function values Evaluate the function at the endpoints of the interval:
- ( f(0) = 0^3 - 2(0^2) + 3(0) - 1 = -1 )
- ( f(1) = 1^3 - 2(1^2) + 3(1) - 1 = 1 )
-
Check domain Since ( f(0) < 0 ) and ( f(1) > 0 ), we confirm there is a root in the interval ([0, 1]).
-
First iteration
- Calculate midpoint: ( c_1 = \frac{0 + 1}{2} = 0.5 )
- Evaluate ( f(c_1) ): $$ f(0.5) = (0.5)^3 - 2(0.5)^2 + 3(0.5) - 1 = 0.125 - 0.5 + 1.5 - 1 = 0.125 $$
- Since ( f(0) < 0) and ( f(0.5) > 0 ), the new interval is ([0, 0.5]).
-
Second iteration
- Calculate new midpoint: ( c_2 = \frac{0 + 0.5}{2} = 0.25 )
- Evaluate ( f(c_2) ): $$ f(0.25) = (0.25)^3 - 2(0.25)^2 + 3(0.25) - 1 = 0.015625 - 0.125 + 0.75 - 1 = -0.359375 $$
- Since ( f(0.25) < 0 ) and ( f(0.5) > 0 ), the new interval is ([0.25, 0.5]).
The root of the function after two iterations is approximately $0.25$.
More Information
The bisection method is a numerical technique used to find roots of continuous functions. By iteratively halving the interval and testing the sign of the function, it converges towards a root.
Tips
- Failing to check if the function changes signs over the interval before applying the bisection method.
- Not rounding the final answer correctly as specified in the problem statement.
AI-generated content may contain errors. Please verify critical information