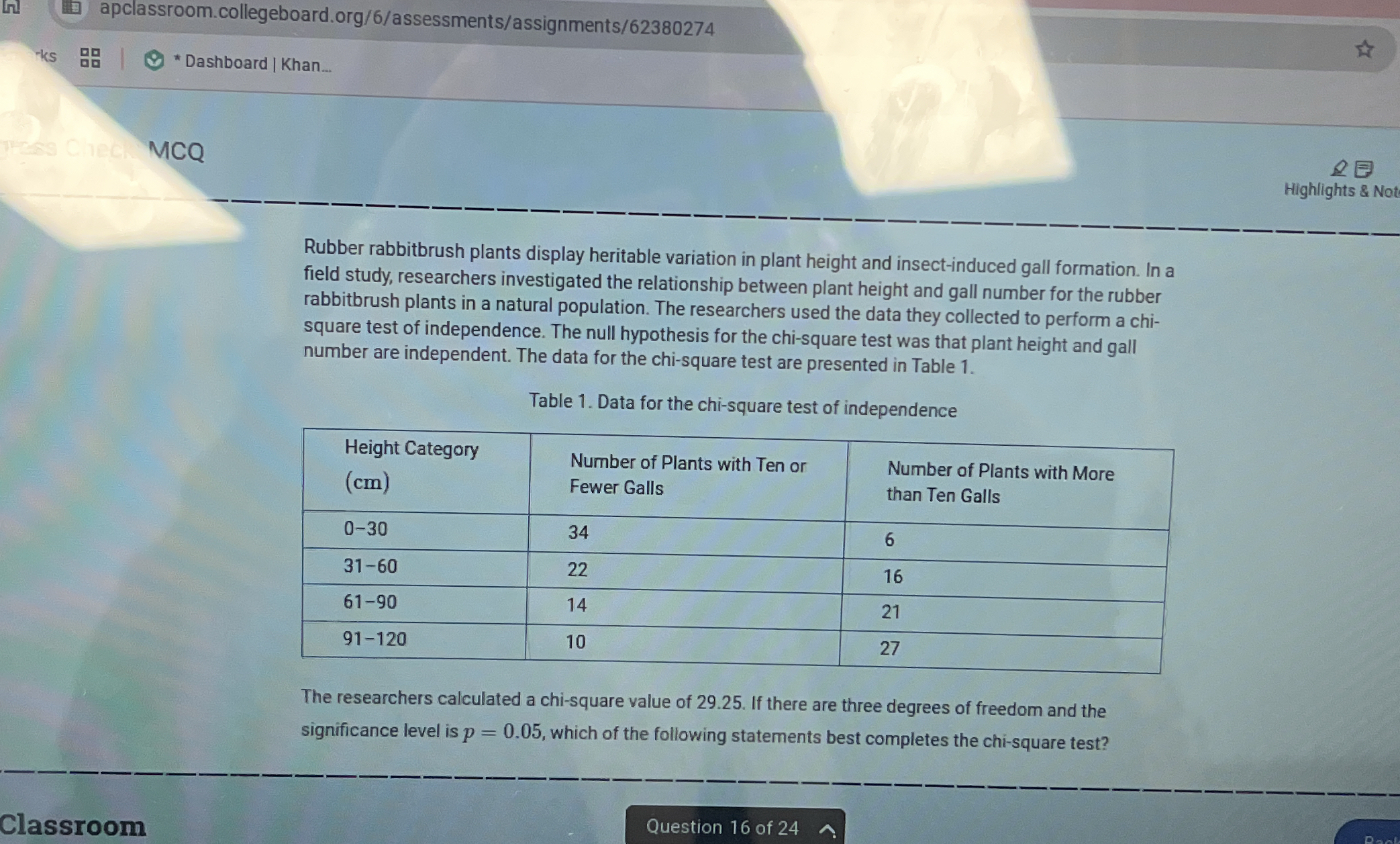
The researchers calculated a chi-square value of 29.25. If there are three degrees of freedom and the significance level is p = 0.05, which of the following statements best complet... The researchers calculated a chi-square value of 29.25. If there are three degrees of freedom and the significance level is p = 0.05, which of the following statements best completes the chi-square test? Read more

Steps to Solve

1. Calculate the Total for Each Height Category First, we need to calculate the total number of plants for each height category by adding the two columns together.

   • For 0-30 cm: $34 + 6 = 40$
   • For 31-60 cm: $22 + 16 = 38$
   • For 61-90 cm: $14 + 21 = 35$
   • For 91-120 cm: $10 + 27 = 37$

2. Calculate the Grand Total of Plants Next, we sum the totals from each height category to get the grand total: $$40 + 38 + 35 + 37 = 150$$

3. Determine Expected Frequencies Using the column totals and the grand total, we can calculate the expected frequency for each cell. The formula is: $$ \text{Expected count} = \frac{\text{Row Total} \times \text{Column Total}}{\text{Grand Total}} $$

   For example, for the 0-30 cm height category and plants with 10 or fewer galls: $$ \text{Expected count} = \frac{40 \times 60}{150} = 16 $$

   Repeat this calculation for each category and each column.

4. Perform the Chi-square Calculation Using the observed values and the expected frequencies, we calculate the chi-square statistic using: $$ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} $$ Where $O_i$ is the observed count and $E_i$ is the expected count for each cell.

5. Compare to Critical Value The critical value for a chi-square test with 3 degrees of freedom (as given) at a significance level of $p = 0.05$ is typically around 7.815. Compare your calculated chi-square value (29.25) against this critical value.

6. Draw Conclusion If the calculated chi-square statistic (29.25) exceeds the critical value (7.815), we reject the null hypothesis. This indicates a significant relationship between plant height and the number of galls.