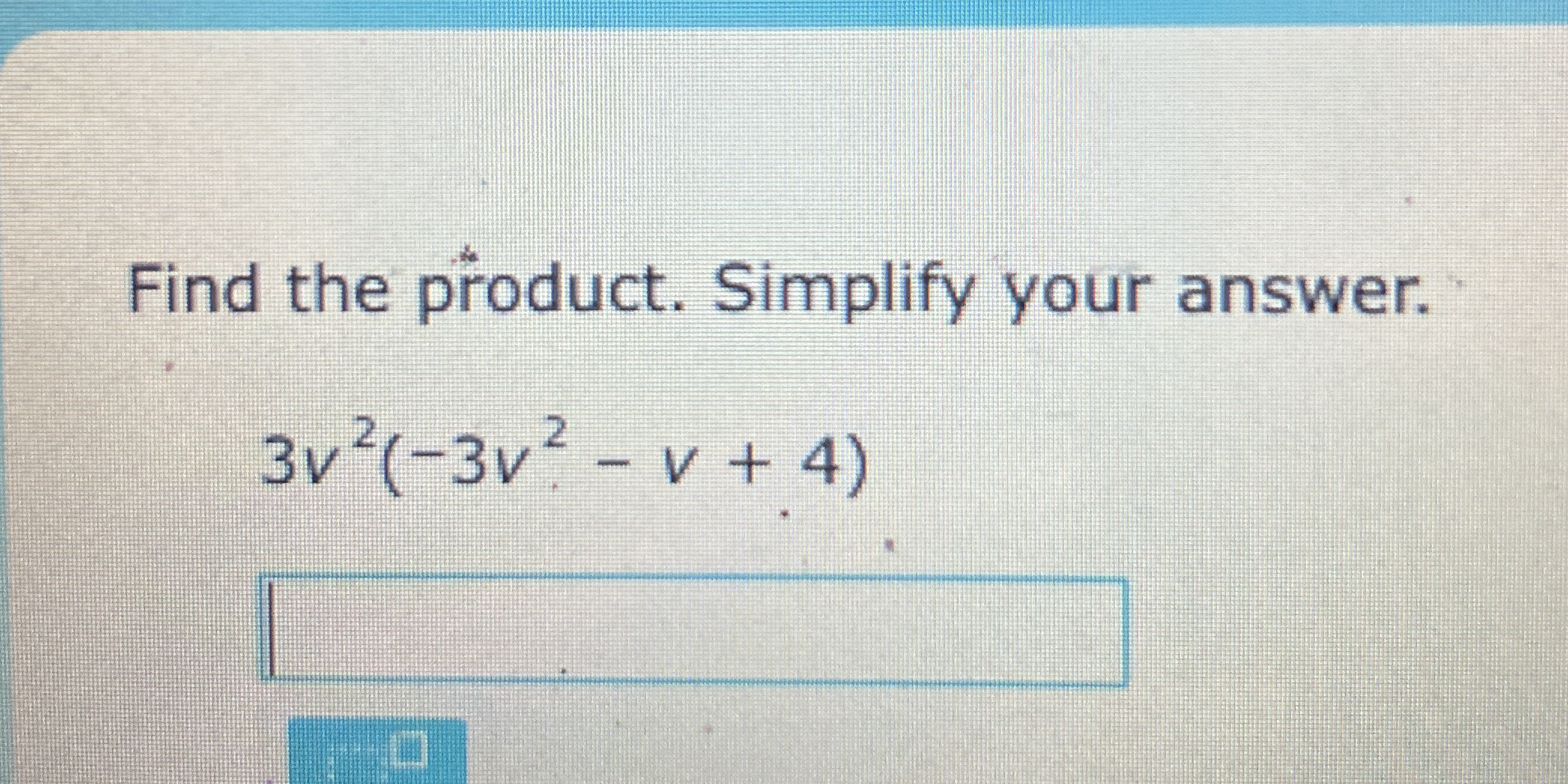
Find the product. Simplify your answer. 3v²(-3v² - v + 4)
Understand the Problem
The question is asking to find the product of the expression given, which includes multiplying a term involving a variable raised to a power with a polynomial, and then simplifying the result.
Answer
The simplified product is $$ -9v^4 - 3v^3 + 12v^2 $$
Answer for screen readers
The simplified product is
$$ -9v^4 - 3v^3 + 12v^2 $$
Steps to Solve
-
Distribute the term
Multiply the term (3v^2) by each term in the polynomial (-3v^2 - v + 4).
First multiply (3v^2) by (-3v^2):
$$ 3v^2 \cdot -3v^2 = -9v^4 $$
-
Continue distributing
Next, multiply (3v^2) by (-v):
$$ 3v^2 \cdot -v = -3v^3 $$
-
Final multiplication
Now, multiply (3v^2) by (4):
$$ 3v^2 \cdot 4 = 12v^2 $$
-
Combine all products
Now, combine the results from all the multiplications:
$$ -9v^4 - 3v^3 + 12v^2 $$
The simplified product is
$$ -9v^4 - 3v^3 + 12v^2 $$
More Information
The product consists of three terms derived from distributing the monomial (3v^2) through the polynomial. Each multiplication respects the exponents of the variable (v), which helps illustrate how polynomial multiplication works.
Tips
- Forgetting to distribute all terms: Ensure each term in the polynomial is multiplied by the leading term.
- Incorrectly handling the signs: Pay attention to the negative signs when multiplying terms, as they can change the sign of the result.
AI-generated content may contain errors. Please verify critical information