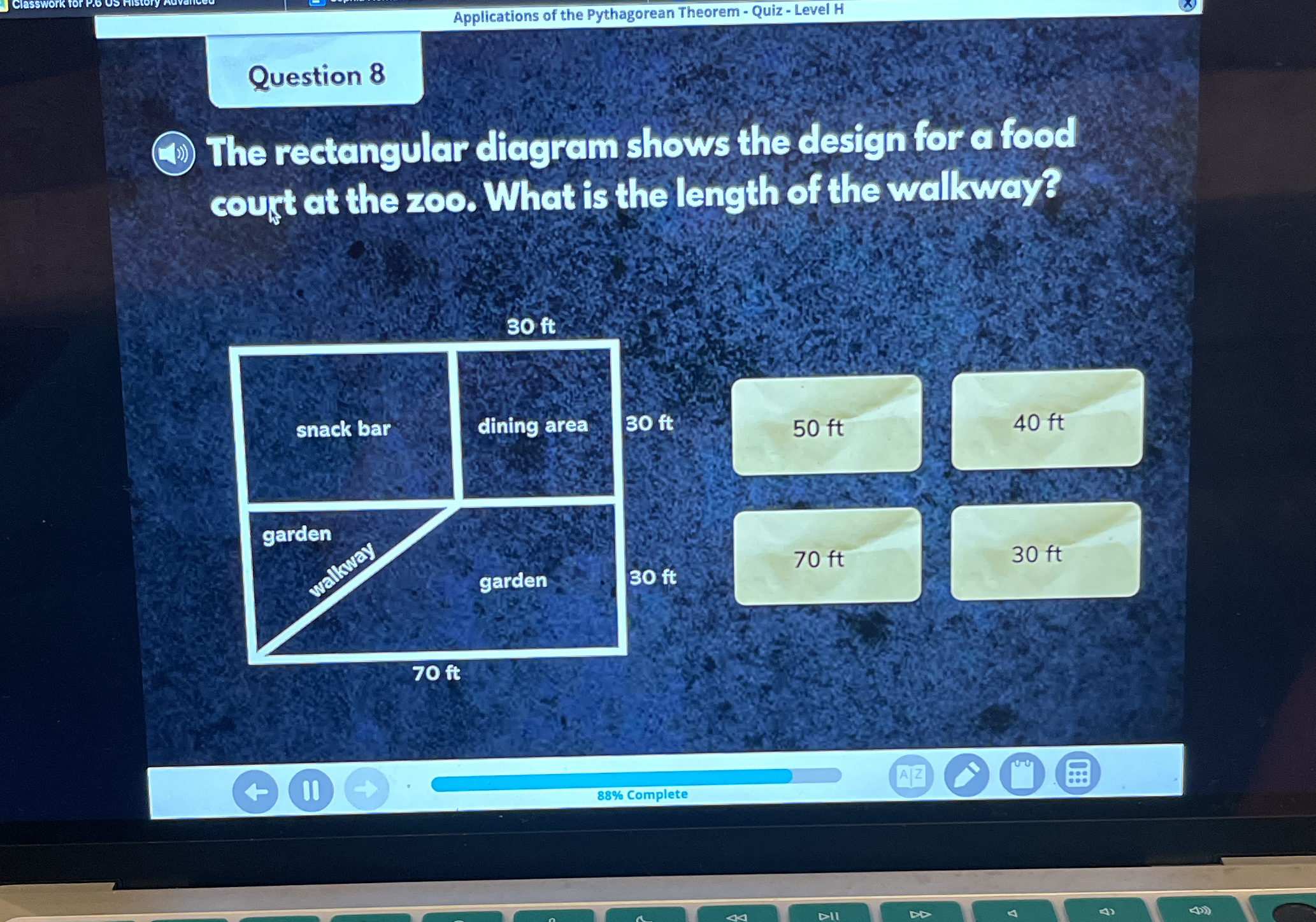
The rectangular diagram shows the design for a food court at the zoo. What is the length of the walkway?

Steps to Solve

1. Identify the sides of the right triangle

The sides are the garden (30 ft), the base of the design (70 ft), and the walkway (hypotenuse).

2. Recall the Pythagorean theorem

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. $$ a^2 + b^2 = c^2 $$ where $c$ is the length of the hypotenuse.

3. Apply the Pythagorean theorem

In this case, let $a = 30$ ft and $b = 70$ ft. Then we can find the length of the walkway $c$ as follows: $$ 30^2 + 70^2 = c^2 $$

4. Calculate the squares $$ 900 + 4900 = c^2 $$

5. Add the values $$ 5800 = c^2 $$

6. Solve for $c$ by taking the square root $$ c = \sqrt{5800} $$

7. Simplify by factoring out the perfect square $$ c = \sqrt{100 \cdot 58} $$ $$ c = \sqrt{100} \cdot \sqrt{58} $$ $$ c = 10 \sqrt{58} \approx 76.16 $$

8. Approximate the value of $\sqrt{5800}$ based on the options provided

Since the exact answer is not among the choices, we should calculate the value and round to the nearest option. $\sqrt{5800} \approx 76.16$. Looking at the food court design, it's important to realize that the base of the right triangle associated with the walkway is equal to $70 - 30 = 40 \text{ ft}$. Using the Pythagorean theorem: $$ 30^2 + 40^2 = c^2 $$ $$ 900 + 1600 = c^2 $$ $$ 2500 = c^2 $$ $$ c = \sqrt{2500} = 50 $$