The radius of a circle is 9 ft. Find its area in terms of π.
Understand the Problem
The question is asking for the area of a circle given its radius. To find the area, we will use the formula A = πr² where r is the radius of the circle. Since the radius is provided as 9 ft, we will substitute this value into the formula.
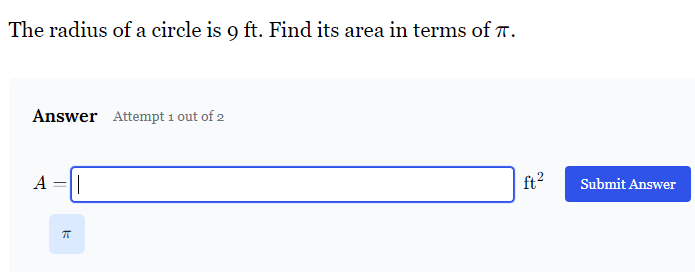
Answer
$A = 81\pi$ ft²
Answer for screen readers
The area of the circle is $81\pi$ ft².
Steps to Solve
- Identify the formula for the area of a circle
The area $A$ of a circle is calculated using the formula:
$$ A = \pi r^2 $$
where $r$ is the radius.
- Substitute the radius into the formula
Given the radius $r = 9$ ft, we substitute this value into the formula:
$$ A = \pi (9)^2 $$
- Calculate the area
Now calculate ( (9)^2 ):
$$ (9)^2 = 81 $$
So,
$$ A = 81\pi $$
The area of the circle is $81\pi$ ft².
More Information
The area of a circle is directly proportional to the square of its radius. This means that if you double the radius, the area increases by a factor of four.
Tips
- Incorrectly squaring the radius: Always ensure you square the radius correctly. Missing this step can lead to incorrect area calculations.
- Forgetting to include $\pi$: Ensure to state the final answer in terms of $\pi$ as requested, avoiding numerical approximations.
AI-generated content may contain errors. Please verify critical information