The product of the eigenvalues of the matrix A = [1 0 0; 0 3 -1; 0 -1 3] is
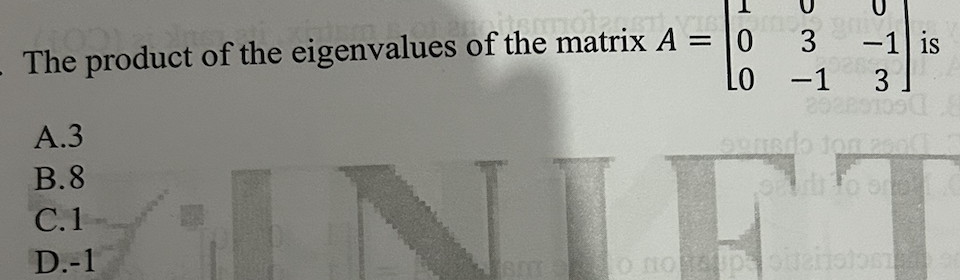
Understand the Problem
The question is asking for the product of the eigenvalues of a given matrix A. To solve this, we will calculate the determinant of the matrix A, as the product of the eigenvalues of a matrix is equal to the determinant of that matrix.
Answer
The product of the eigenvalues of the matrix \( A \) is \( 8 \).
Answer for screen readers
The product of the eigenvalues of the matrix ( A ) is ( 8 ).
Steps to Solve
- Identify the Matrix A
Given the matrix ( A ): $$ A = \begin{pmatrix} 1 & 0 & 0 \ 0 & 3 & -1 \ 0 & -1 & 3 \end{pmatrix} $$
- Calculate the Determinant of A
To find the determinant of matrix ( A ), we can use the formula for a 3x3 matrix. The determinant is calculated as follows:
$$ \text{det}(A) = a(ei-fh) - b(di-fg) + c(dh-eg) $$
For matrix ( A ):
- ( a = 1, b = 0, c = 0 )
- ( d = 0, e = 3, f = -1 )
- ( g = 0, h = -1, i = 3 )
Plugging in the values: $$ \text{det}(A) = 1 \cdot (3 \cdot 3 - (-1) \cdot (-1)) - 0 + 0 $$ Calculating: $$ \text{det}(A) = 1 \cdot (9 - 1) = 1 \cdot 8 = 8 $$
- Interpret Calculation Result
Since the product of the eigenvalues of a matrix is equal to its determinant, we have: $$ \text{Product of eigenvalues} = \text{det}(A) = 8 $$
The product of the eigenvalues of the matrix ( A ) is ( 8 ).
More Information
The determinant provides an important property of a matrix: it gives us information about the product of its eigenvalues. For matrix ( A ), which is a block matrix, the computation simplifies due to the zero entries.
Tips
- A common mistake is incorrectly applying the determinant formula for 3x3 matrices. Ensure to systematically identify elements according to their positions.
- Another mistake can be overlooking that the product of the eigenvalues is equal to the determinant.
AI-generated content may contain errors. Please verify critical information