The points (4, 1) and (8, 2.5) are on the line with equation y = -1/2x + 4. M is the midpoint of AB. Find an equation of the line through M that is perpendicular to y = -1/2x + 4.
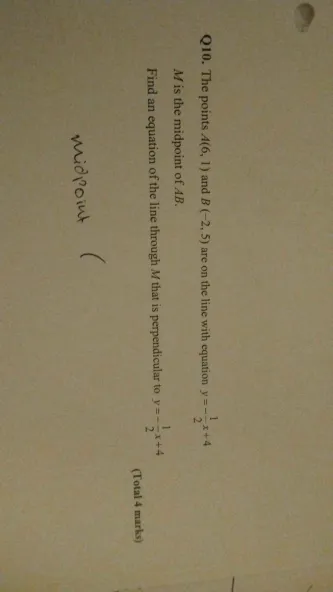
Understand the Problem
The question is asking to find the equation of a line that passes through the midpoint of the points (4, 1) and (8, 2.5), and is perpendicular to the line described by the equation y = -1/2x + 4. This involves calculating the midpoint and then determining the slope of the perpendicular line to find its equation.
Answer
The equation of the line is \( y = 2x - 10.25 \).
Answer for screen readers
The equation of the line through the midpoint ( M(6, 1.75) ) that is perpendicular to the line ( y = -\frac{1}{2}x + 4 ) is: $$ y = 2x - 10.25 $$
Steps to Solve
-
Calculate the Midpoint M To find the midpoint ( M ) of the points ( (4, 1) ) and ( (8, 2.5) ), we use the midpoint formula: $$ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) $$ Substituting the coordinates: $$ M = \left( \frac{4 + 8}{2}, \frac{1 + 2.5}{2} \right) = \left( \frac{12}{2}, \frac{3.5}{2} \right) = (6, 1.75) $$
-
Identify the Slope of the Given Line The equation of the given line is ( y = -\frac{1}{2}x + 4 ). From this, we identify the slope ( m_1 = -\frac{1}{2} ).
-
Find the Slope of the Perpendicular Line The slope of the line that is perpendicular to another is the negative reciprocal of the original slope. Therefore, the slope ( m_2 ) of the perpendicular line is: $$ m_2 = -\frac{1}{m_1} = -\frac{1}{-\frac{1}{2}} = 2 $$
-
Use the Point-Slope Form to Find the Equation Now that we have the slope ( m_2 = 2 ) and the point ( M(6, 1.75) ), we can use the point-slope form of the line: $$ y - y_1 = m(x - x_1) $$ Substituting ( m_2 ) and the coordinates of ( M ): $$ y - 1.75 = 2(x - 6) $$
-
Simplify to Standard Form Now, we simplify the equation: $$ y - 1.75 = 2x - 12 $$ Adding ( 1.75 ) to both sides results in: $$ y = 2x - 10.25 $$
The equation of the line through the midpoint ( M(6, 1.75) ) that is perpendicular to the line ( y = -\frac{1}{2}x + 4 ) is: $$ y = 2x - 10.25 $$
More Information
The midpoint is a crucial point in geometry, and finding the slope of a perpendicular line involves finding the negative reciprocal. This approach is widely applicable in coordinate geometry.
Tips
- Forgetting to use the negative reciprocal when finding the slope of the perpendicular line.
- Simplifying the equation incorrectly after applying the point-slope form.
AI-generated content may contain errors. Please verify critical information