The number of distinct real roots of (x - 2)^4 + (x + 2)^4 = 392 is
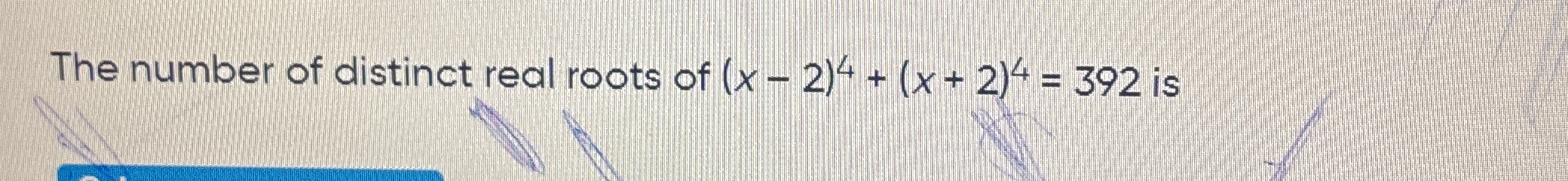
Understand the Problem
The question is asking for the number of distinct real roots of the equation involving fourth powers of terms that are expressions in x, equated to 392. It requires analysis and possibly solving for x to determine the count of distinct real solutions.
Answer
2
Answer for screen readers
The number of distinct real roots is 2.
Steps to Solve
- Rewrite the equation
Start with the equation:
$$(x - 2)^4 + (x + 2)^4 = 392$$
- Introduce a substitution
Let:
$$u = (x - 2)^2 + (x + 2)^2$$
Then rewrite it as:
$$u = (x - 2)^2 + (x + 2)^2 = (x^2 - 4x + 4 + x^2 + 4x + 4) = 2x^2 + 8$$
- Express the original equation in terms of $u$
Now, express the original equation using $u$:
$$(x - 2)^4 + (x + 2)^4 = u^2 - 16u + 64$$
Set it equal to 392:
$$u^2 - 16u + 64 = 392$$
- Simplify the equation
Reorganize it:
$$u^2 - 16u - 328 = 0$$
- Use the quadratic formula
Now apply the quadratic formula, $u = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$:
Here, $a = 1$, $b = -16$, and $c = -328$.
Calculate the discriminant:
$$D = b^2 - 4ac = (-16)^2 - 4(1)(-328) = 256 + 1312 = 1568$$
- Solve for $u$
Now substitute the values into the quadratic formula:
$$u = \frac{16 \pm \sqrt{1568}}{2}$$
Calculating $\sqrt{1568}$ gives approximately $39.6$:
$$u = \frac{16 \pm 39.6}{2}$$
This yields two values:
-
$$u_1 = \frac{55.6}{2} \approx 27.8$$
-
$$u_2 = \frac{-23.6}{2} \approx -11.8$$ (not valid, since $u$ must be non-negative)
-
Back to $x$ and finding roots
Now, substitute back into $u = 2x^2 + 8$:
$$27.8 = 2x^2 + 8$$
Rearranging gives:
$$2x^2 = 19.8 \implies x^2 = 9.9 \implies x = \pm \sqrt{9.9}$$
Thus, we have two distinct real roots.
The number of distinct real roots is 2.
More Information
This problem illustrates the method of substitution and utilizing the quadratic formula to find solutions to a polynomial equation. The initial equation involved quartics, but simplifying through substitution led to a quadratic that was solvable.
Tips
- Confusing the substitution step and miscalculating $u$.
- Not accounting for negative roots while considering $u$.
- Failing to double-check the discriminant when using the quadratic formula.
AI-generated content may contain errors. Please verify critical information