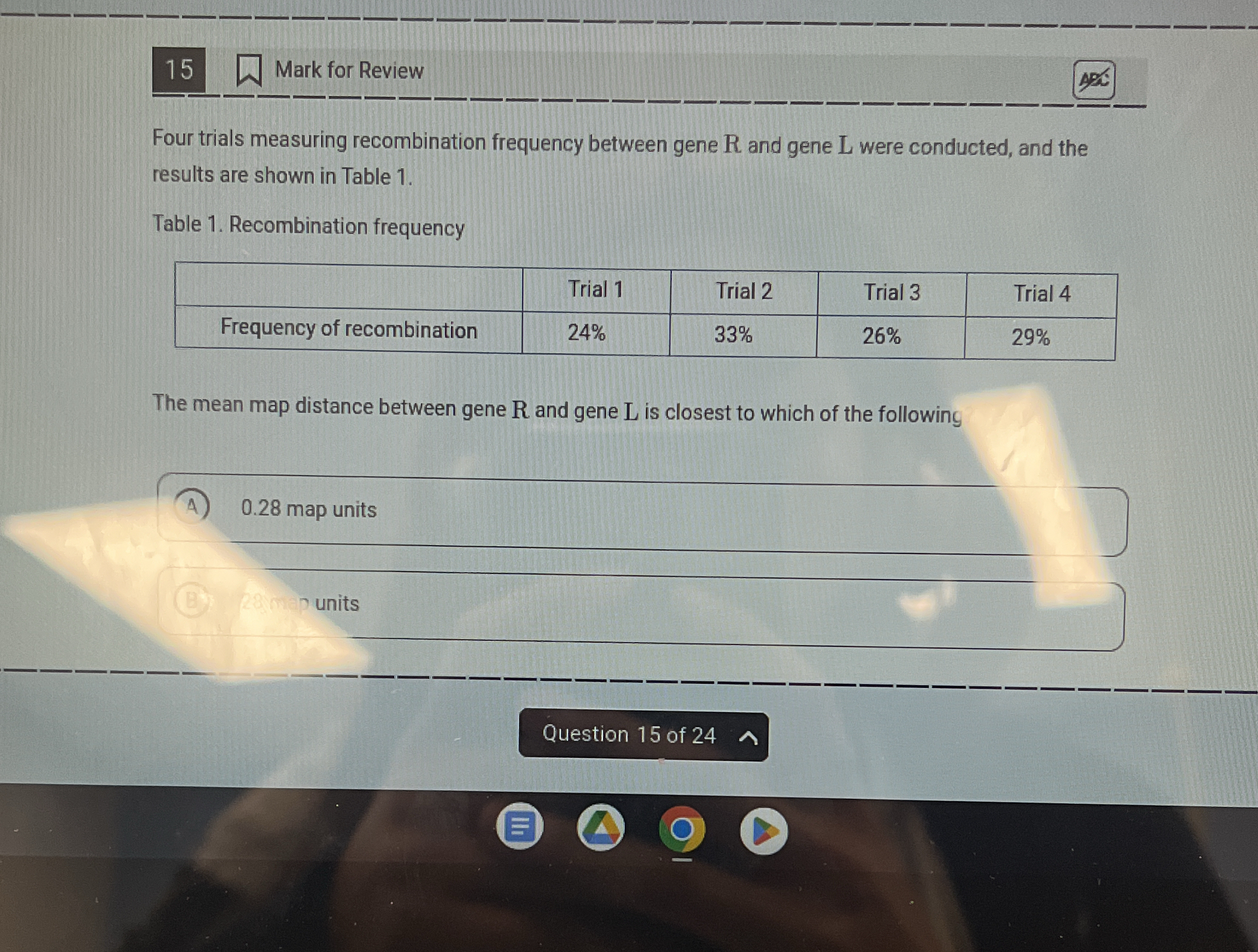
The mean map distance between gene R and gene L is closest to which of the following?
Understand the Problem
The question is asking for the mean map distance between gene R and gene L based on provided recombination frequencies from four trials. To solve this, we need to calculate the mean of the given percentages and then convert that into map units, which is defined as the percentage of recombination frequency.
Answer
The mean map distance is $28$ map units.
Answer for screen readers
The mean map distance between gene R and gene L is $28$ map units.
Steps to Solve
-
List the recombination frequencies The given recombination frequencies from each trial are:
Trial 1: 24%
Trial 2: 33%
Trial 3: 26%
Trial 4: 29% -
Calculate the sum of the frequencies Add the frequencies together:
$$ 24% + 33% + 26% + 29% = 112% $$ -
Calculate the mean frequency Divide the total by the number of trials to find the mean frequency:
$$ \text{Mean} = \frac{112%}{4} = 28% $$ -
Convert the mean frequency to map units Since 1% recombination frequency equals 1 map unit, the mean map distance is:
$$ \text{Map Distance} = 28 \text{ map units} $$
The mean map distance between gene R and gene L is $28$ map units.
More Information
Map units are a measure of genetic distance based on the frequency of recombination, with 1% recombination frequency corresponding to 1 map unit. The calculated mean provides an average measure of how far apart the genes are in terms of recombination likelihood.
Tips
- Forgetting to divide the total frequency by the number of trials.
- Miscalculating the sum of the frequencies.
- Confusing percentage with actual map units.
AI-generated content may contain errors. Please verify critical information