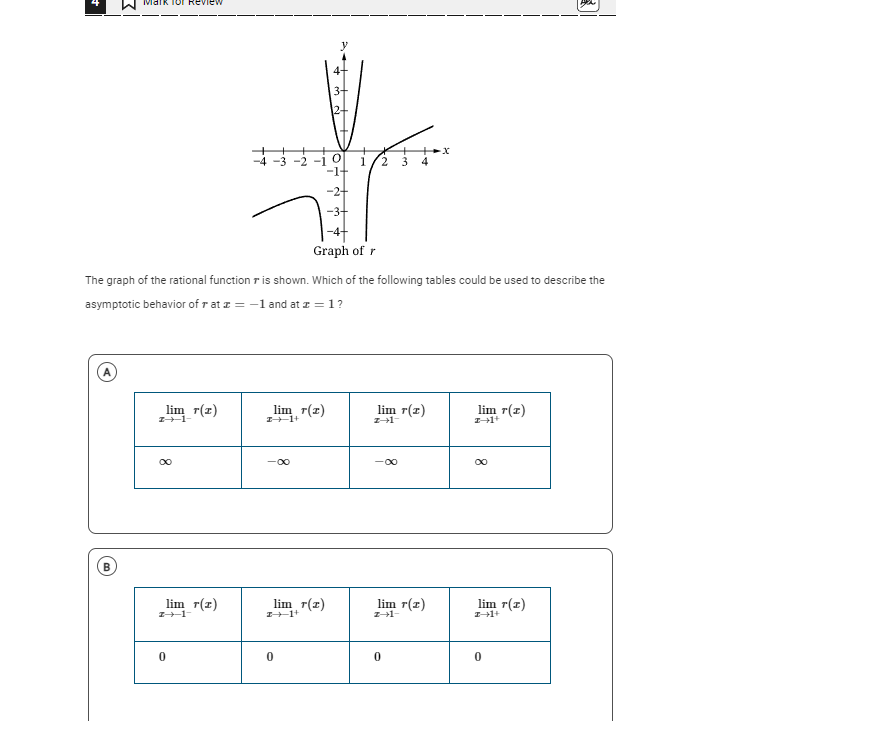
The graph of the rational function r is shown. Which of the following tables could be used to describe the asymptotic behavior of r at x = -1 and at x = 1?

Steps to Solve

1. Analyze the Graph at ( x = -1 )

Look at the behavior of the graph as ( x ) approaches -1. The graph appears to have a vertical asymptote at this point, indicating that as ( x ) approaches -1 from the left, ( r(x) ) goes to ( -\infty ), and as ( x ) approaches -1 from the right, ( r(x) ) goes to ( +\infty ).

Thus, we conclude: $$ \lim_{x \to -1^-} r(x) = -\infty $$ $$ \lim_{x \to -1^+} r(x) = +\infty $$

2. Analyze the Graph at ( x = 1 )

Now, observe the graph as ( x ) approaches 1. The behavior indicates that ( r(x) ) approaches a finite number from both sides (it appears to approach the value of 0).

Therefore, we conclude: $$ \lim_{x \to 1^-} r(x) = 0 $$ $$ \lim_{x \to 1^+} r(x) = 0 $$

3. Summarize the Limits

In summary, the limits can be represented as follows:

• At ( x = -1 ):

  • ( \lim_{x \to -1^-} r(x) = -\infty )
  • ( \lim_{x \to -1^+} r(x) = +\infty )

• At ( x = 1 ):

  • ( \lim_{x \to 1^-} r(x) = 0 )
  • ( \lim_{x \to 1^+} r(x) = 0 )

4. Match the Findings with the Tables

Based on the analysis above, the correct limits match with Table A:

• ( \lim_{x \to -1^-} r(x) = -\infty )
• ( \lim_{x \to -1^+} r(x) = +\infty )
• ( \lim_{x \to 1^-} r(x) = 0 )
• ( \lim_{x \to 1^+} r(x) = 0 )