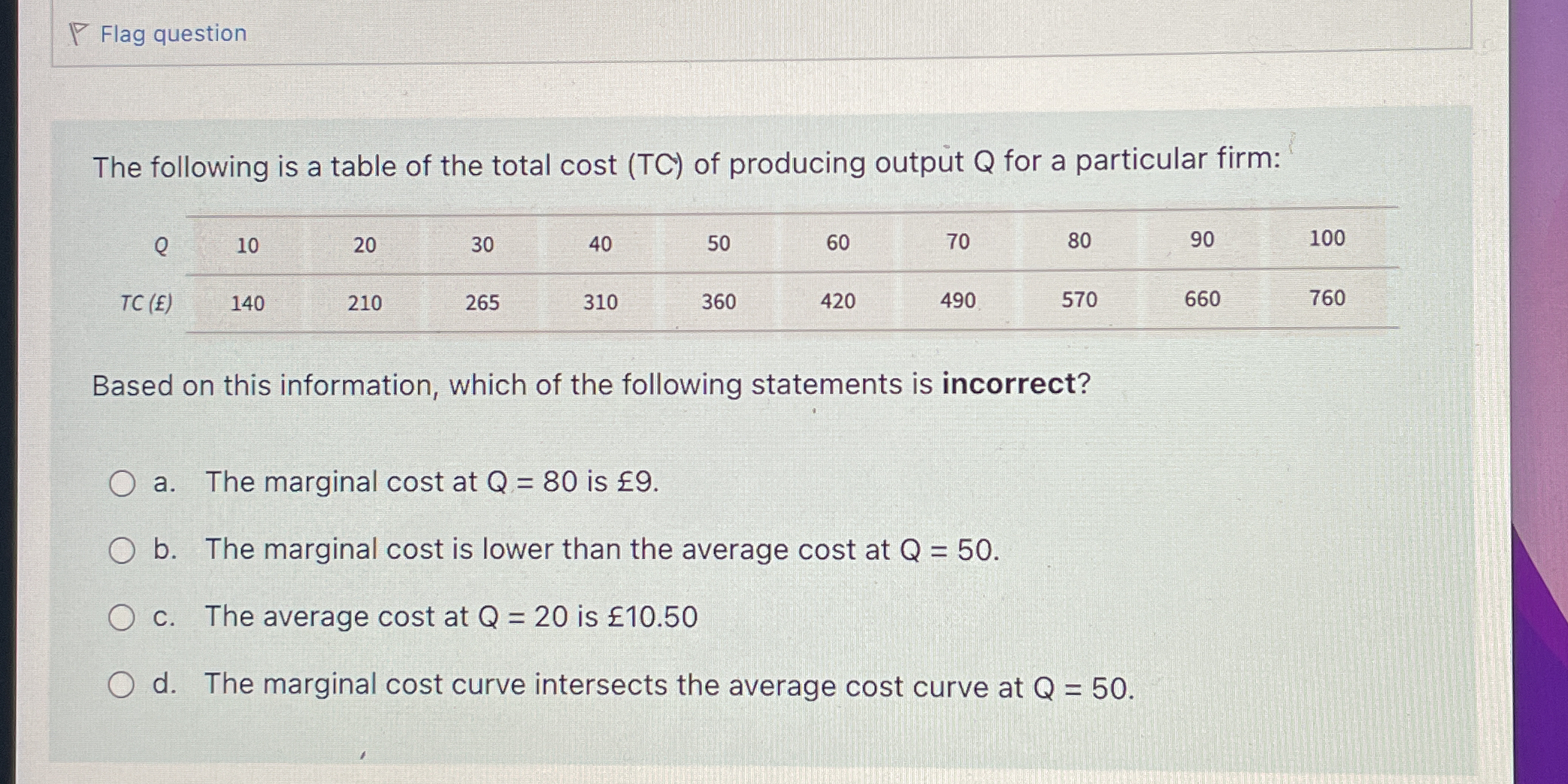
The following is a table of the total cost (TC) of producing output Q for a particular firm: Q 10 20 30 40 50 60 70 80 90 100 TC (£) 140 210 265 310 360 420 490 570 660 760 Based o... The following is a table of the total cost (TC) of producing output Q for a particular firm: Q 10 20 30 40 50 60 70 80 90 100 TC (£) 140 210 265 310 360 420 490 570 660 760 Based on this information, which of the following statements is incorrect? a. The marginal cost at Q = 80 is £9. b. The marginal cost is lower than the average cost at Q = 50. c. The average cost at Q = 20 is £10.50 d. The marginal cost curve intersects the average cost curve at Q = 50.
Understand the Problem
The question presents data regarding total costs associated with different output levels for a firm. It asks which of the given statements about marginal cost and average cost based on this data is incorrect.
Answer
The incorrect statement is (d): The marginal cost curve intersects the average cost curve at $Q = 50$.
Answer for screen readers
The incorrect statement is (d): The marginal cost curve intersects the average cost curve at $Q = 50$.
Steps to Solve
- Calculate Marginal Cost (MC)
Marginal cost is calculated as the change in total cost divided by the change in quantity produced. For instance, to find the marginal cost from $Q = 70$ to $Q = 80$:
- Total Cost at $Q = 70$ is £570
- Total Cost at $Q = 80$ is £660
[ MC = \frac{TC_{80} - TC_{70}}{Q_{80} - Q_{70}} = \frac{660 - 570}{80 - 70} = \frac{90}{10} = £9 ]
- Verify Statement a - MC at Q = 80
From the calculation above, the marginal cost at $Q = 80$ is indeed £9, so statement (a) is correct.
- Calculate Average Cost (AC) for Q = 50
To find the average cost, divide the total cost by the quantity produced. For $Q = 50$:
- Total Cost at $Q = 50$ is £360.
[ AC = \frac{TC}{Q} = \frac{360}{50} = £7.20 ]
- Calculate Marginal Cost for Q = 50
To find the marginal cost at $Q = 50$, look at the change from $Q = 40$ to $Q = 50$:
- Total Cost at $Q = 40$ is £310
[ MC = \frac{TC_{50} - TC_{40}}{Q_{50} - Q_{40}} = \frac{360 - 310}{50 - 40} = \frac{50}{10} = £5 ]
- Verify Statement b - Compare MC and AC at Q = 50
Here, marginal cost £5 is lower than average cost £7.20, so statement (b) is also correct.
- Calculate Average Cost (AC) at Q = 20
To find the average cost for $Q = 20$:
- Total Cost at $Q = 20$ is £210.
[ AC = \frac{TC}{Q} = \frac{210}{20} = £10.50 ]
- Verify Statement c - AC at Q = 20
Since the calculation shows average cost at $Q = 20$ as £10.50, statement (c) is correct.
- Check Statement d - Marginal Cost Intersects AC at Q = 50
Marginal cost equals average cost at the minimum point of the average cost curve. Since we've calculated that at $Q = 50$, AC (£7.20) does not equal MC (£5). Therefore, statement (d) must be the incorrect statement as it implies a necessary intersection.
The incorrect statement is (d): The marginal cost curve intersects the average cost curve at $Q = 50$.
More Information
The relationship between marginal cost and average cost is fundamental in economics; MC intersects AC at its minimum point. When MC is below AC, it pulls AC down. Conversely, when MC is above AC, it pulls AC up.
Tips
- Miscalculating average or marginal cost by not correctly applying the formulas.
- Confusing where to find marginal cost (change between two total costs) versus average cost (total cost divided by quantity).
AI-generated content may contain errors. Please verify critical information