The expansion of the determinant along the second row is:
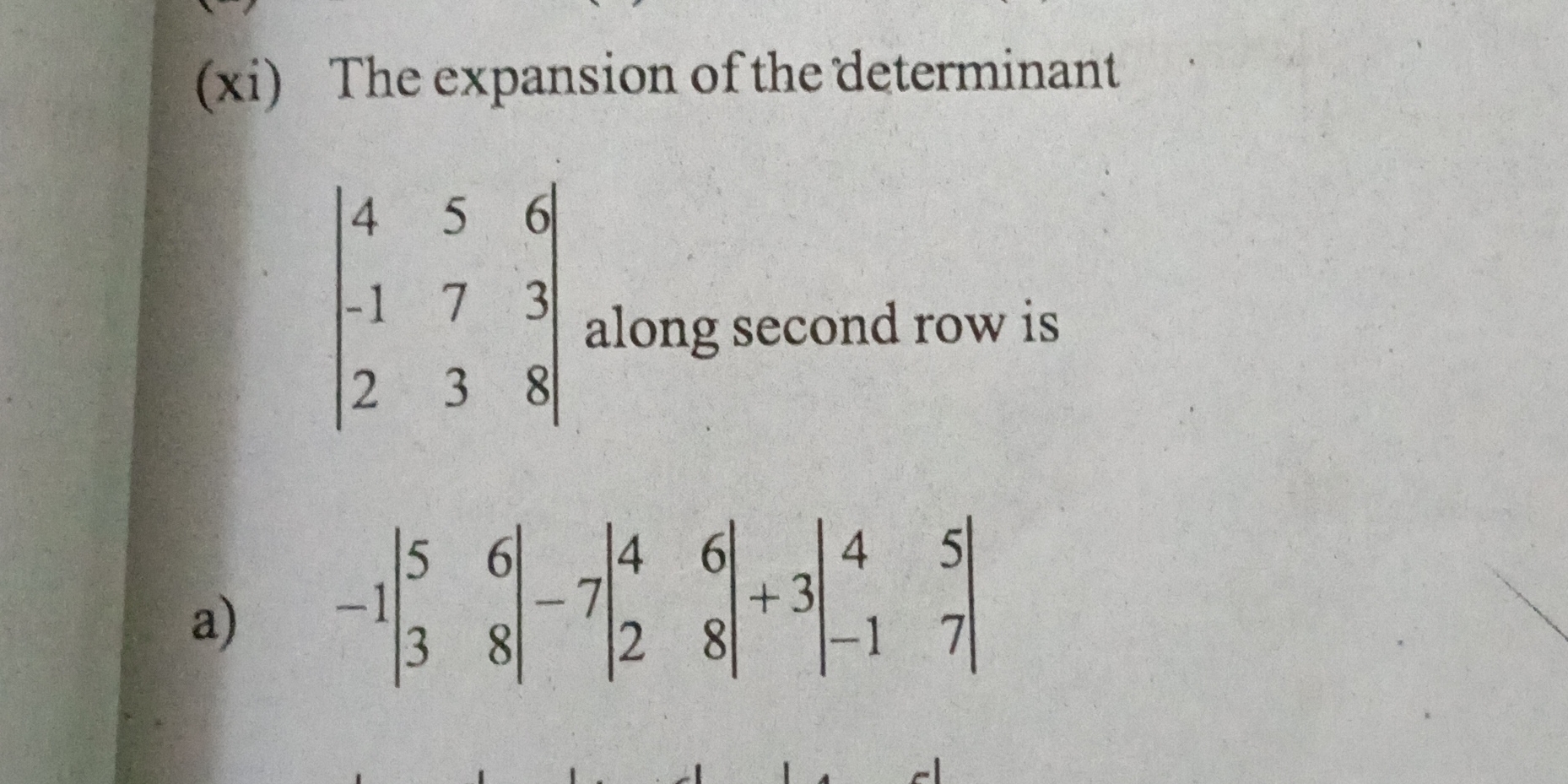
Understand the Problem
The question is asking for the expansion of a given determinant along the second row, specifically how to calculate it using the determinant's first and second rows.
Answer
The expansion of the determinant along the second row is $124$.
Answer for screen readers
The expansion of the determinant along the second row is $124$.
Steps to Solve
- Identify the determinant and its entries
The determinant to be expanded is given as:
$$ D = \begin{vmatrix} 4 & 5 & 6 \ -1 & 7 & 3 \ 2 & 3 & 8 \end{vmatrix} $$
- Use the second row for expansion
For the expansion along the second row, we will use the formula:
$$ D = a_{21} \cdot D_{21} + a_{22} \cdot D_{22} + a_{23} \cdot D_{23} $$
where $a_{ij}$ are the elements of the second row and $D_{ij}$ are the corresponding minors.
- Calculate the determinants of minors
- First Element: $a_{21} = -1$
The minor $D_{21}$ is:
$$ D_{21} = \begin{vmatrix} 5 & 6 \ 3 & 8 \end{vmatrix} = (5 \cdot 8) - (6 \cdot 3) = 40 - 18 = 22 $$
- Second Element: $a_{22} = 7$
The minor $D_{22}$ is:
$$ D_{22} = \begin{vmatrix} 4 & 6 \ 2 & 8 \end{vmatrix} = (4 \cdot 8) - (6 \cdot 2) = 32 - 12 = 20 $$
- Third Element: $a_{23} = 3$
The minor $D_{23}$ is:
$$ D_{23} = \begin{vmatrix} 4 & 5 \ 2 & 3 \end{vmatrix} = (4 \cdot 3) - (5 \cdot 2) = 12 - 10 = 2 $$
- Putting it all together
Now plug in the values:
$$ D = (-1) \cdot 22 + 7 \cdot 20 + 3 \cdot 2 $$
Calculating gives:
$$ D = -22 + 140 + 6 = 124 $$
The expansion of the determinant along the second row is $124$.
More Information
The value of a determinant represents the volume scaling factor of the linear transformation described by the matrix. In this case, it indicates how the area is transformed in the context of the vectors represented by the matrix.
Tips
- Not calculating the minors correctly. Always double-check the determinant of the 2x2 matrices.
- Forgetting to apply the alternating signs for the cofactor expansion. Remember to alternate signs starting with the first element being negative.
AI-generated content may contain errors. Please verify critical information