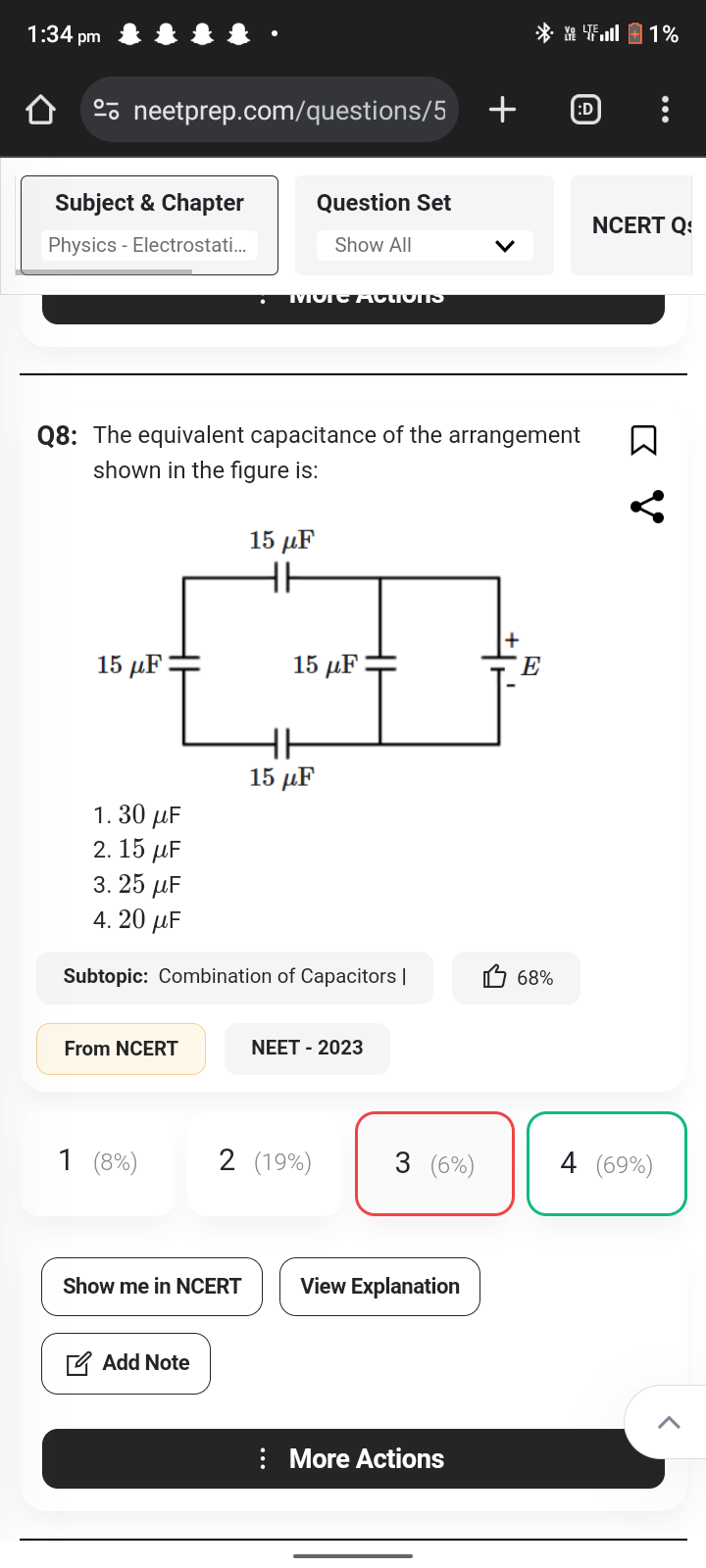
The equivalent capacitance of the arrangement shown in the figure is:
Understand the Problem
The question is asking for the equivalent capacitance of a specific arrangement of capacitors shown in a figure. It presents several answer options to choose from, which involves applying principles of electrical circuits, particularly the combination of capacitors.
Answer
The equivalent capacitance is $20 \, \mu F$.
Answer for screen readers
The equivalent capacitance of the arrangement is $20 , \mu F$.
Steps to Solve
- Identify the configuration of capacitors
In the circuit, we have three capacitors of $15 , \mu F$ each on the left side in series and one $15 , \mu F$ capacitor on the right side in parallel with them.
- Calculate the equivalent capacitance for the series group
The formula for capacitors in series is given by:
$$ \frac{1}{C_{eq, series}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} $$
For three capacitors of $15 , \mu F$:
$$ \frac{1}{C_{eq, series}} = \frac{1}{15} + \frac{1}{15} + \frac{1}{15} = \frac{3}{15} $$
Therefore, the equivalent capacitance for the series group is:
$$ C_{eq, series} = \frac{15}{3} = 5 , \mu F $$
- Add the parallel capacitor's capacitance
Next, we add the equivalent capacitance of the series group to the capacitance of the parallel capacitor. The formula for capacitors in parallel is:
$$ C_{eq, total} = C_{eq, series} + C_{parallel} $$
So,
$$ C_{eq, total} = 5 , \mu F + 15 , \mu F = 20 , \mu F $$
The equivalent capacitance of the arrangement is $20 , \mu F$.
More Information
In this arrangement of capacitors, the connection type affects the equivalent capacitance significantly. For series combinations, the total capacitance decreases, while for parallel combinations, it increases.
Tips
- Forgetting the difference between series and parallel configurations can lead to errors in calculation.
- Not simplifying the fractions correctly when calculating equivalent capacitance for capacitors in series.