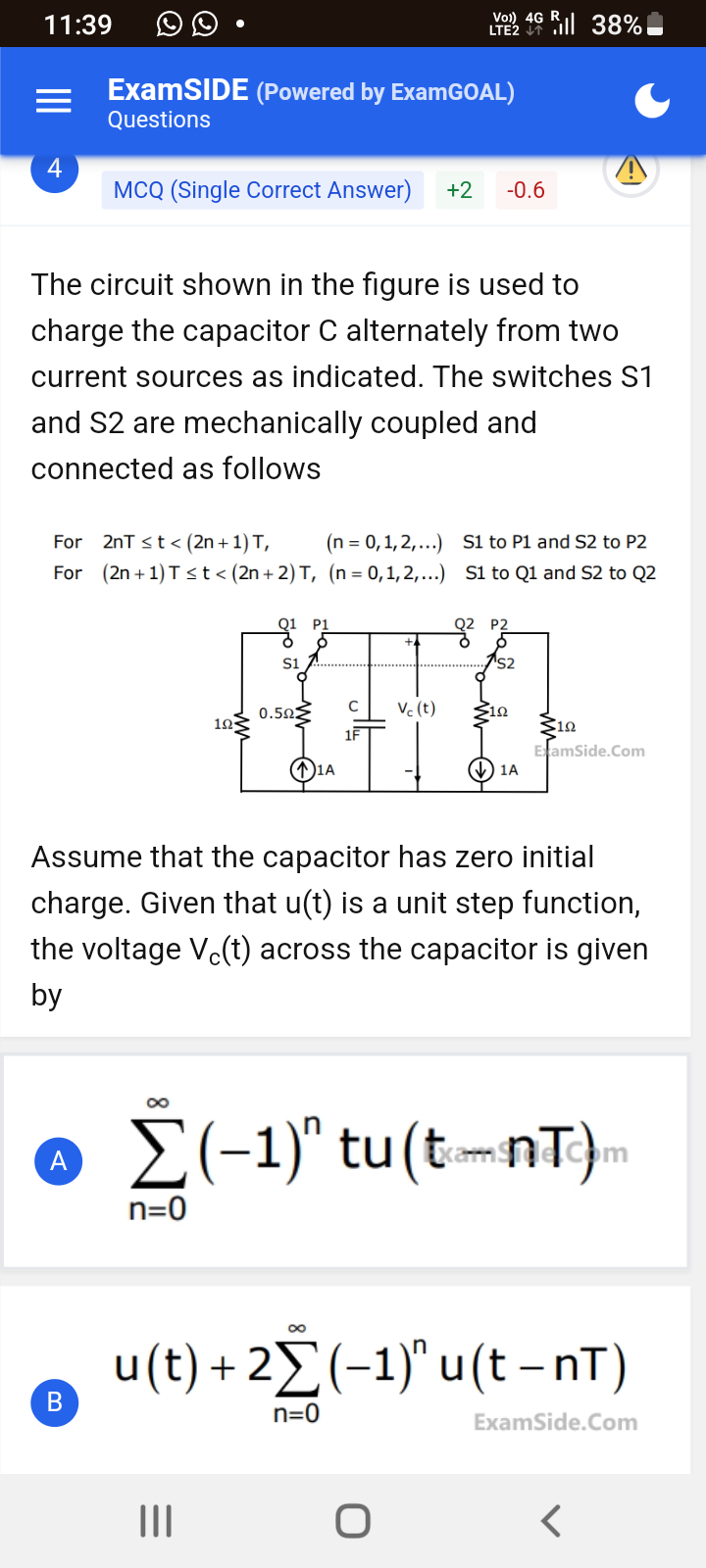
The circuit shown in the figure is used to charge the capacitor C alternately from two current sources as indicated. The switches S1 and S2 are mechanically coupled and connected a... The circuit shown in the figure is used to charge the capacitor C alternately from two current sources as indicated. The switches S1 and S2 are mechanically coupled and connected as follows. Assume that the capacitor has zero initial charge. Given that u(t) is a unit step function, the voltage Vc(t) across the capacitor is given by:
Understand the Problem
The question involves analyzing an electrical circuit with capacitors and switches to determine the voltage across a capacitor over time, given specific conditions and a mathematical function. The problem requires an understanding of electrical engineering concepts, particularly in circuit analysis.
Answer
The voltage across the capacitor is given by: $$ V_c(t) = \sum_{n=0}^{\infty} (-1)^n u(t - nT) $$
Answer for screen readers
The correct expression for the voltage across the capacitor $V_c(t)$ is: $$ V_c(t) = \sum_{n=0}^{\infty} (-1)^n u(t - nT) $$
Steps to Solve
- Identify the Function for Voltage Across the Capacitor
The problem states that $u(t)$ is a unit step function, and the voltage across the capacitor $V_c(t)$ is to be expressed using this function.
- Understand the Behavior of the Circuit
The circuit charges the capacitor alternatively, implying that the voltage across it will change periodically based on the operation of the switches $S1$ and $S2$.
- Define the Series of Voltages Over Time
Given the periodic nature (in terms of $nT$), we can express $V_c(t)$ as a sum: $$ V_c(t) = \sum_{n=0}^{\infty} (-1)^n u(t - nT) $$ This represents alternating contributions to the voltage as time progresses.
- Consider the Initial Conditions
Since the initial charge on the capacitor is zero, the initial conditions simplify the expression to begin calculating from the first time switch changes.
- Analyze the Options Provided
We compare the derived expression with the given options to determine which correctly represents $V_c(t)$ across the capacitor.
The correct expression for the voltage across the capacitor $V_c(t)$ is: $$ V_c(t) = \sum_{n=0}^{\infty} (-1)^n u(t - nT) $$
More Information
The capacitor in the circuit exhibits a behavior where its voltage oscillates between values due to alternating current sources. The unit step function, $u(t)$, helps model when the voltage updates due to switch actions over time.
Tips
- Mixing up the behavior of the unit step function and applying it incorrectly in time intervals.
- Not accounting for the initial condition (zero initial charge) affecting the overall voltage function.
- Confusing the indices when summing the voltages; ensure correct limits and signs.
AI-generated content may contain errors. Please verify critical information