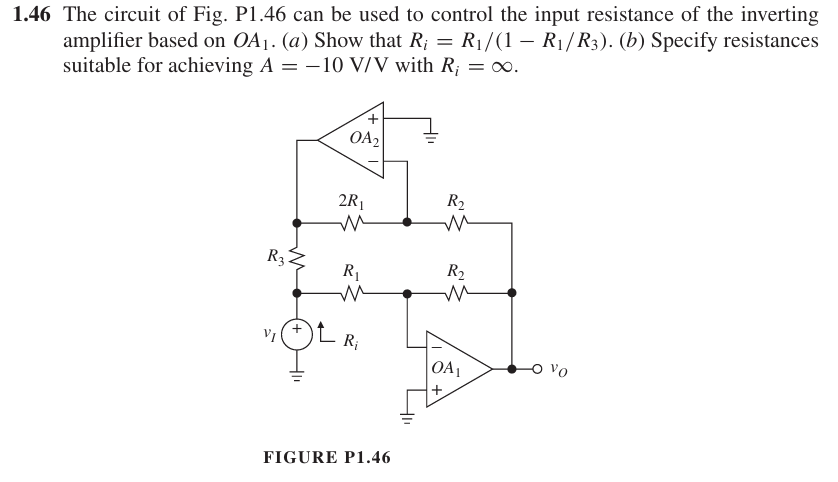
The circuit of Fig. P1.46 can be used to control the input resistance of the inverting amplifier based on OA1. (a) Show that Ri = R1/(1 - R1/R3). (b) Specify resistances suitable f... The circuit of Fig. P1.46 can be used to control the input resistance of the inverting amplifier based on OA1. (a) Show that Ri = R1/(1 - R1/R3). (b) Specify resistances suitable for achieving A = -10 V/V with Ri = ∞. Read more

Steps to Solve

1. Understanding the Inverting Amplifier Configuration

The inverting amplifier gain $A$ is given by the formula: $$ A = -\frac{R_f}{R_{in}} $$ where $R_f$ is the feedback resistor and $R_{in}$ is the input resistor. In this case, we have additional components $R_1$, $R_2$, $R_3$, and $R_i$ affecting the input resistance $R_i$.

2. Deriving Input Resistance Expression

To derive the input resistance $R_i$, we apply the relationship given in the problem: $$ R_i = \frac{R_1}{1 - \frac{R_1}{R_3}} $$ This can be rearranged to highlight how $R_1$ and $R_3$ influence $R_i$.

3. Finding Suitable Resistor Values for Gain

We need a gain of $A = -10$. From the gain formula: $$ -10 = -\frac{R_f}{R_{in}} $$ We can choose $R_f = 10R_{in}$. To meet the requirement of $R_i = \infty$, we consider suitable values of resistors.

4. Selecting Resistor Values

By setting $R_i$ (or $R_{in}$) as an arbitrary value, let’s say $R_{in} = 1 k\Omega$, then: $$ R_f = 10 \times R_{in} = 10 k\Omega $$ Select $R_1$ and $R_3$ such that they satisfy the above relationship, we can set $R_1 = 1 k\Omega$ and $R_3 = 0 k\Omega$ to keep $R_i = \infty$.