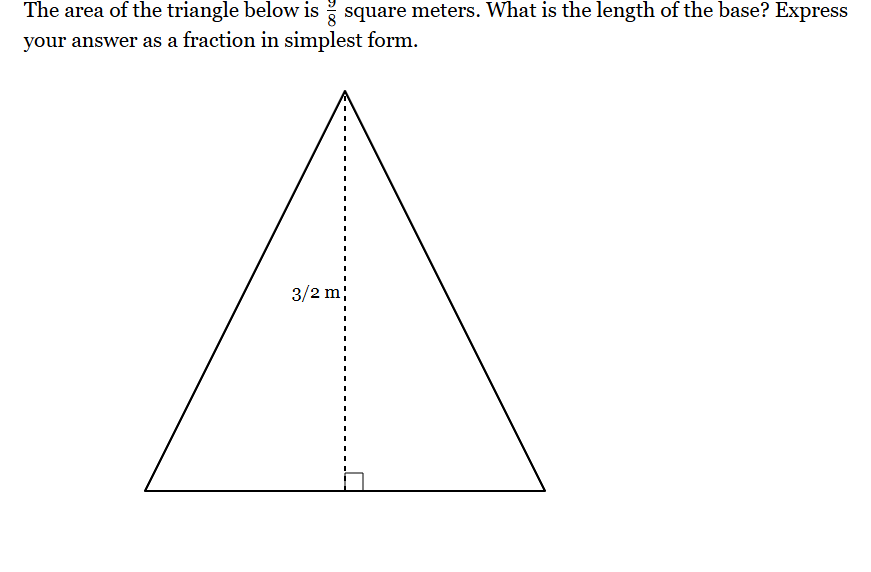
The area of the triangle below is 5/8 square meters. What is the length of the base? Express your answer as a fraction in simplest form.

Steps to Solve

1. Write down the formula for the area of a triangle

The formula for the area of a triangle is:

$$ A = \frac{1}{2} \times \text{base} \times \text{height} $$

2. Substitute the values into the formula

We know the area ($A$) is $\frac{5}{8}$ square meters and the height is $\frac{3}{2}$ meters. Substitute these values into the formula:

$$ \frac{5}{8} = \frac{1}{2} \times \text{base} \times \frac{3}{2} $$

3. Simplify the equation

Multiply both sides by 2 to eliminate the fraction on the right side:

$$ 2 \times \frac{5}{8} = \text{base} \times \frac{3}{2} $$

This simplifies to:

$$ \frac{5}{4} = \text{base} \times \frac{3}{2} $$

4. Solve for the base

To isolate the base, multiply both sides by the reciprocal of $\frac{3}{2}$:

$$ \text{base} = \frac{5}{4} \div \frac{3}{2} $$

This can be written as:

$$ \text{base} = \frac{5}{4} \times \frac{2}{3} $$

5. Multiply to find the base length

Now multiply the fractions:

$$ \text{base} = \frac{5 \times 2}{4 \times 3} = \frac{10}{12} $$

6. Simplify the fraction

Simplify $\frac{10}{12}$:

$$ \text{base} = \frac{5}{6} $$