τ = z + λ(9) + x(4) - 61 = z + x (in an equation format)
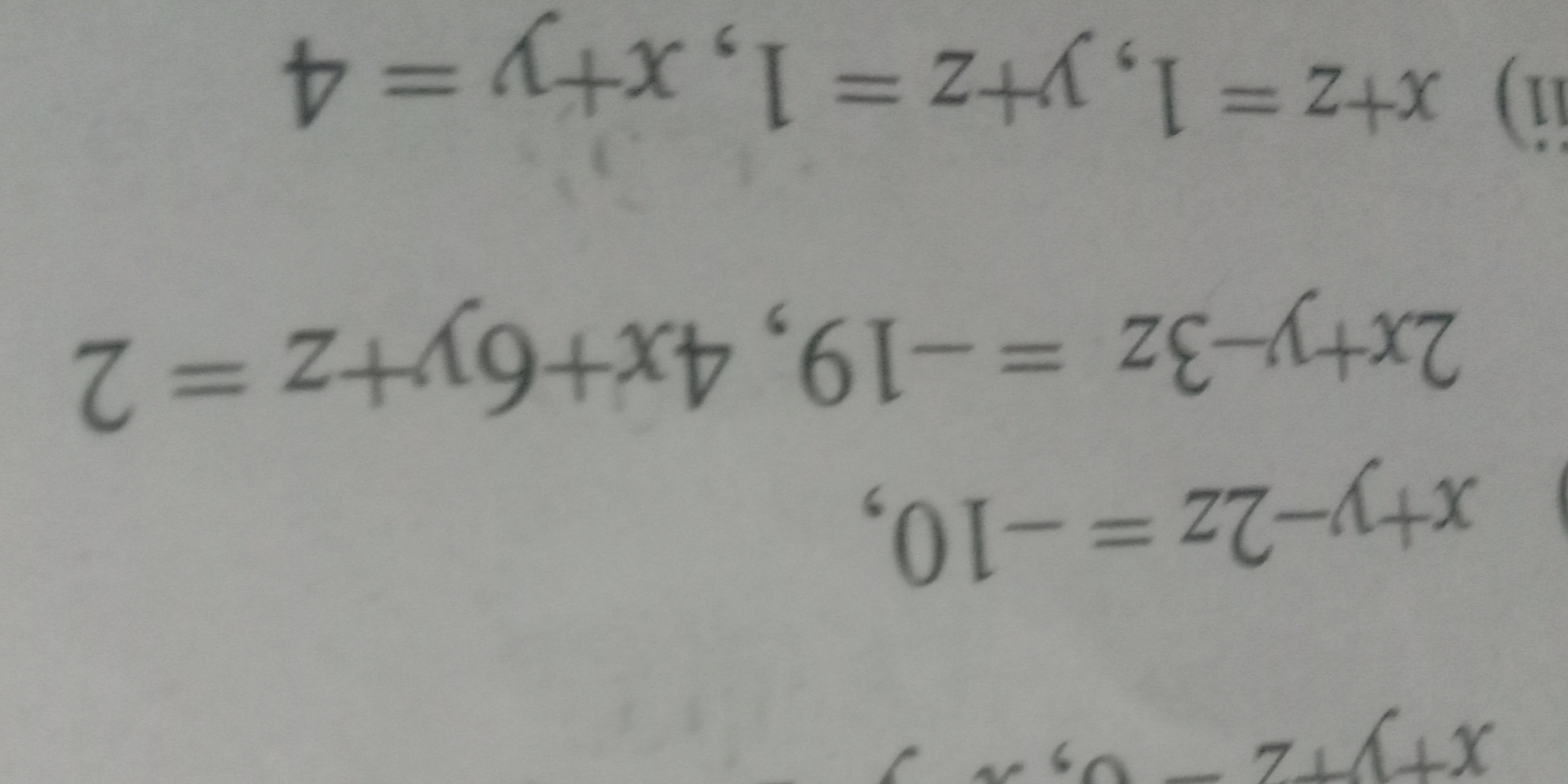
Understand the Problem
The question appears to involve mathematical relationships or equations involving variables such as z and x. It likely requires solving or simplifying the equations presented.
Answer
$$ x = \frac{61 - 9\lambda}{3} $$
Answer for screen readers
The final expression for $x$ is given by:
$$ x = \frac{61 - 9\lambda}{3} $$
Steps to Solve
- Set Up the Equation
Start with the equation provided:
$$ \tau = z + \lambda(9) + x(4) - 61 = z + x $$
- Simplify the Left Side
Rearrange the equation:
$$ z + \lambda(9) + 4x - 61 = z + x $$
- Isolate Terms Involving Variables
Eliminate $z$ from both sides:
$$ \lambda(9) + 4x - 61 = x $$
- Move x Term to One Side
Subtract $x$ from both sides:
$$ \lambda(9) + 4x - x - 61 = 0 $$
which simplifies to:
$$ \lambda(9) + 3x - 61 = 0 $$
- Rearrange to Solve for x
Bring the constant to the other side:
$$ 3x = 61 - \lambda(9) $$
- Solve for x
Divide by 3:
$$ x = \frac{61 - \lambda(9)}{3} $$
- Substitute Back If Needed
If you need to find specific values for $x$ or $\lambda$, substitute them into the final equation.
The final expression for $x$ is given by:
$$ x = \frac{61 - 9\lambda}{3} $$
More Information
This result shows how $x$ depends on the variable $\lambda$. If you have specific values for $\lambda$, you can substitute them into the equation to find corresponding values for $x$.
Tips
- Neglecting to isolate variables: Ensure you are correctly moving terms across the equals sign.
- Misplacing constants during simplification: Double-check arithmetic operations to avoid errors in terms of signs or values.
AI-generated content may contain errors. Please verify critical information