Suppose E is an elementary matrix formed by performing k*r20 + r17, for k ∈ ℝ, on the corresponding identity matrix, in which entry will there be k?
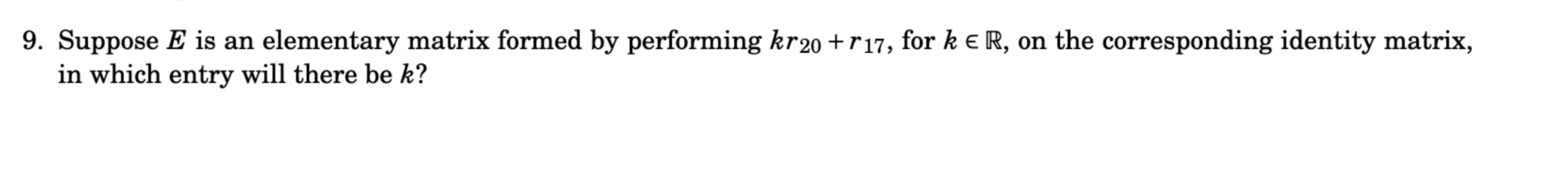
Understand the Problem
The question is asking about the specific entry in an elementary matrix formed by a linear combination of the rows of an identity matrix. It involves understanding how elementary matrices are constructed and how the index of the rows affects the resulting matrix.
Answer
The entry containing $k$ is at position $(17, 20)$.
Answer for screen readers
The entry containing $k$ is located in position $(17, 20)$ of the matrix.
Steps to Solve
-
Identify the Operation
The operation performed is $k \cdot r_{20} + r_{17}$. This means we are taking a multiple of row 20 and adding it to row 17 of the identity matrix. -
Identify the Structure of the Elementary Matrix
An elementary matrix is derived from the identity matrix $I_n$ by applying a row operation. For the operation mentioned, we will modify the identity matrix specifically. -
Position of k in the Matrix
In the identity matrix, the elements outside the diagonal are zero. When we perform the operation $k \cdot r_{20} + r_{17}$, the coefficient $k$ will replace the corresponding position of row 17 in column 20.
Thus, in the final elementary matrix $E$, the entry of interest, where you will find $k$, is at position $(17, 20)$.
The entry containing $k$ is located in position $(17, 20)$ of the matrix.
More Information
Elementary matrices are useful in performing row operations on matrices. The specific entry's position indicates where the row operation affects the identity matrix, and understanding this paves the way for grasping more complex matrix operations.
Tips
- Not identifying the correct row and column: When performing row operations, always ensure you have the right row indices in mind.
- Confusing row operations with column operations: Since the operation affects rows, it's crucial to remember that the changes occur in specified row positions, not column positions.
