Solve: (x^2 + y^2 - a^2)dx + (x^2 - y^2 - b^2)dy = 0
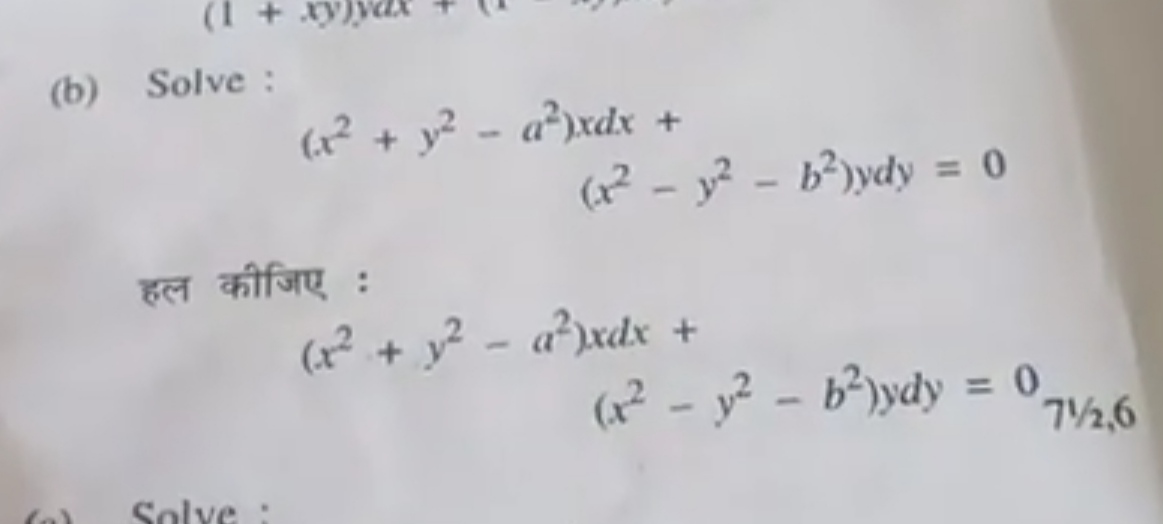
Understand the Problem
The question asks to solve a differential equation involving terms with variables x and y, as well as constants a and b. The equation is structured as a sum of terms equating to zero, suggesting an application of calculus techniques to find solutions or relationships between the variables.
Answer
The solution is an implicit relationship between \( x \) and \( y \) derived from the differential equation.
Answer for screen readers
The solution involves finding an implicit relationship between ( x ) and ( y ) that satisfies:
$$ F(x,y) = C $$
where ( F ) is derived from the integrated form of the differential equation.
Steps to Solve
-
Rearrange the Differential Equation
We start with the given equation:
$$(x^2 + y^2 - a^2)dx + (x^2 - y^2 - b^2)dy = 0$$
We can organize it into the form:
$$ (x^2 + y^2 - a^2) \frac{dx}{dy} + (x^2 - y^2 - b^2) = 0 $$ -
Separate Variables
To solve for $\frac{dx}{dy}$, we isolate it: $$ \frac{dx}{dy} = -\frac{x^2 - y^2 - b^2}{x^2 + y^2 - a^2} $$ -
Integrate Both Sides
Next, we separate variables: $$ \frac{dx}{x^2 + y^2 - a^2} = -\frac{(x^2 - y^2 - b^2)}{(y^2 + x^2 - a^2)} dy $$
Now we integrate both sides, applying appropriate integration techniques. -
Perform Integration
Integrate the left side and the right side to find the general solution. Let’s denote: $$ u = x^2 + y^2 - a^2 $$ $$ dv = (x^2 - y^2 - b^2) dy $$ -
Use Integration Techniques
Use integration methods such as substitution or partial fractions to solve the integrals. -
Substitute Back
After integrating, substitute back the original variables $x$ and $y$ to express the solution in the original terms. -
Include Constants of Integration
Don’t forget to include the constant of integration $C$ based on the context or boundary conditions provided.
The solution involves finding an implicit relationship between ( x ) and ( y ) that satisfies:
$$ F(x,y) = C $$
where ( F ) is derived from the integrated form of the differential equation.
More Information
This differential equation represents a family of curves in the ( xy )-plane, depending on the constants ( a ) and ( b ). The solution can represent circles or ellipses based on the quadratic forms of ( x ) and ( y ).
Tips
- Not properly separating variables before integrating.
- Forgetting to include the constant of integration after integrating.
- Misapplying integration techniques (e.g., not recognizing perfect squares).
AI-generated content may contain errors. Please verify critical information