Solve using substitution: -8x - 3y = -10; -8x + y = -18.
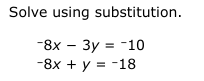
Understand the Problem
The question is asking us to solve a system of equations using the substitution method. We will isolate one variable in one equation and substitute it into the other equation to find the values of both variables.
Answer
The solution is \( (x, y) = (2, -2) \).
Answer for screen readers
The solution to the system of equations is ( x = 2 ) and ( y = -2 ).
Steps to Solve
-
Isolate one variable Let's isolate ( y ) in the second equation: [ -8x + y = -18 ] Rearranging gives: [ y = 8x - 18 ]
-
Substitute the isolated variable Next, we substitute ( y ) into the first equation: [ -8x - 3(8x - 18) = -10 ] Distributing ( -3 ) results in: [ -8x - 24x + 54 = -10 ]
-
Combine like terms Combining the ( x ) terms: [ -32x + 54 = -10 ]
-
Solve for ( x ) Now, we'll isolate ( x ): [ -32x = -10 - 54 ] [ -32x = -64 ] Dividing both sides by ( -32 ): [ x = 2 ]
-
Substitute ( x ) back to find ( y ) Now that we have ( x ), we substitute back to find ( y ): [ y = 8(2) - 18 ] [ y = 16 - 18 ] [ y = -2 ]
The solution to the system of equations is ( x = 2 ) and ( y = -2 ).
More Information
This solution shows how the substitution method can effectively solve systems of linear equations. The values of ( x ) and ( y ) can be verified by plugging them back into the original equations.
Tips
- Forgetting to distribute correctly when substituting values.
- Miscalculating when combining like terms; double-check each arithmetic operation to avoid errors.
AI-generated content may contain errors. Please verify critical information