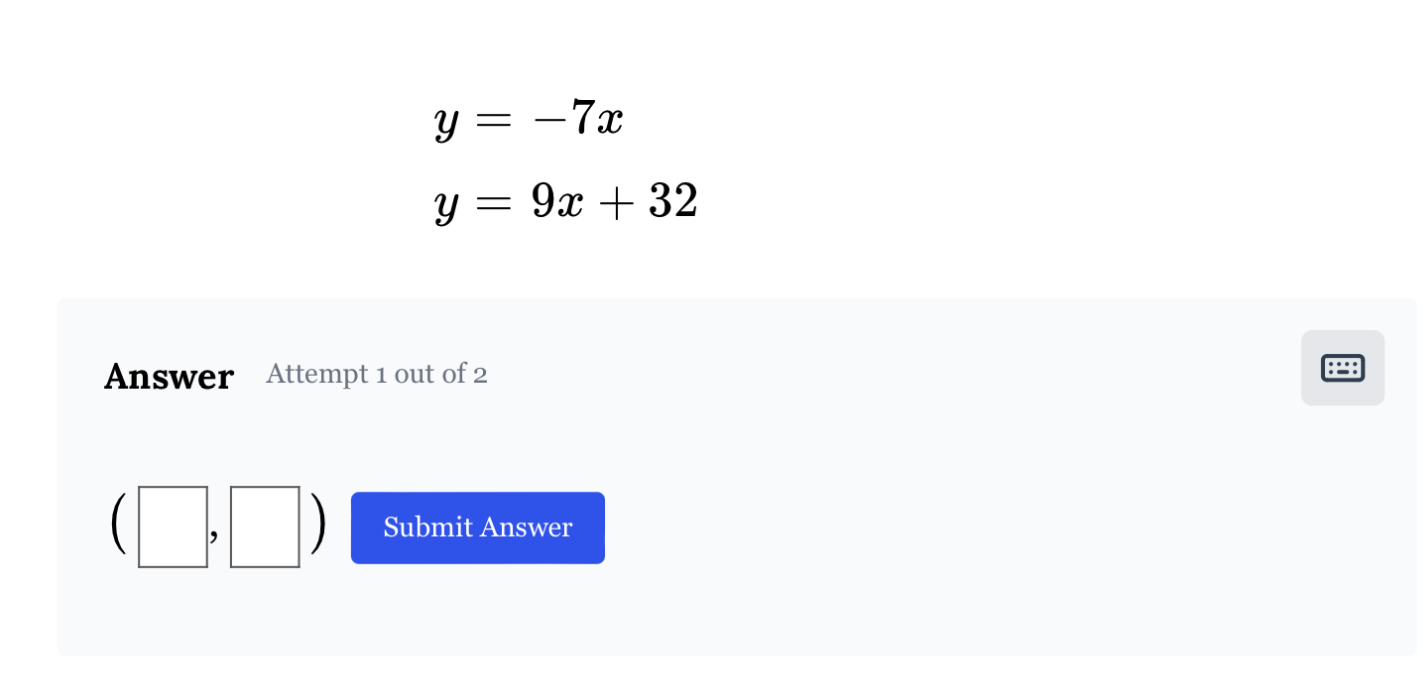
Solve the system of equations: y = -7x and y = 9x + 32.

Understand the Problem

The question is asking to find the solution for the system of equations given by y = -7x and y = 9x + 32. This involves finding the values of x and y that satisfy both equations simultaneously.

Answer

$(-2, 14)$

Steps to Solve

Set the equations equal to each other

Since both equations equal $y$, we can set them equal to each other: $$ -7x = 9x + 32 $$

Isolate the variable $x$

We will isolate $x$ by moving $9x$ to the left side: $$ -7x - 9x = 32 $$

This simplifies to: $$ -16x = 32 $$

Solve for $x$

Now, divide both sides by $-16$: $$ x = \frac{32}{-16} $$ $$ x = -2 $$

Substitute $x$ back into one of the original equations

We can substitute $x = -2$ into the first equation $y = -7x$: $$ y = -7(-2) $$ $$ y = 14 $$

Write the final solution

The solution to the system of equations is the ordered pair: $$ (x, y) = (-2, 14) $$

The final answer is $(-2, 14)$.

More Information

The solution $(-2, 14)$ means that if we substitute $x = -2$ into either of the original equations, we will get $y = 14$. This point represents where the two lines intersect on a graph.

Tips

Common mistakes include:

Miscalculating when isolating variables (e.g., forgetting to change the sign).
Confusing the substitution step and using an incorrect equation.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!