Solve the system of equations using elimination: -5x + 8y = 5 and x - 2y = 1.
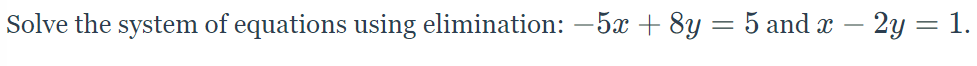
Understand the Problem
The question is asking us to solve the given system of linear equations using the elimination method. This involves manipulating the equations to eliminate one variable, allowing us to solve for the other variable.
Answer
The solution is \( x = -9 \) and \( y = -5 \).
Answer for screen readers
The solution to the system of equations is ( x = -9 ) and ( y = -5 ).
Steps to Solve
- Align the equations for elimination
We have the system: [ \begin{align*} -5x + 8y &= 5 \quad \text{(1)} \ x - 2y &= 1 \quad \text{(2)} \end{align*} ]
- Multiply the equations to align coefficients
To eliminate $x$, multiply equation (2) by 5, creating a new equation: [ 5(x - 2y) = 5(1) ] This gives us: [ 5x - 10y = 5 \quad \text{(3)} ]
- Add the modified equations
Now, add equation (1) and equation (3): [ (-5x + 8y) + (5x - 10y) = 5 + 5 ] This simplifies to: [ -2y = 10 ]
- Solve for $y$
Divide both sides by -2: [ y = -5 ]
- Substitute $y$ back into one of the original equations
Now, substituting $y = -5$ into equation (2): [ x - 2(-5) = 1 ] This simplifies to: [ x + 10 = 1 ]
- Solve for $x$
Subtract 10 from both sides: [ x = 1 - 10 = -9 ]
The solution to the system of equations is ( x = -9 ) and ( y = -5 ).
More Information
The solution represents the point of intersection for the two lines represented by the equations. In a graphical interpretation, this point is where both equations are satisfied simultaneously.
Tips
- Misaligning coefficients: Be diligent in aligning the coefficients properly when manipulating the equations.
- Arithmetic errors: Double-check calculations when adding/subtracting equations.
- Incorrect substitution: Ensure proper substitution of values back into the remaining equations.
AI-generated content may contain errors. Please verify critical information