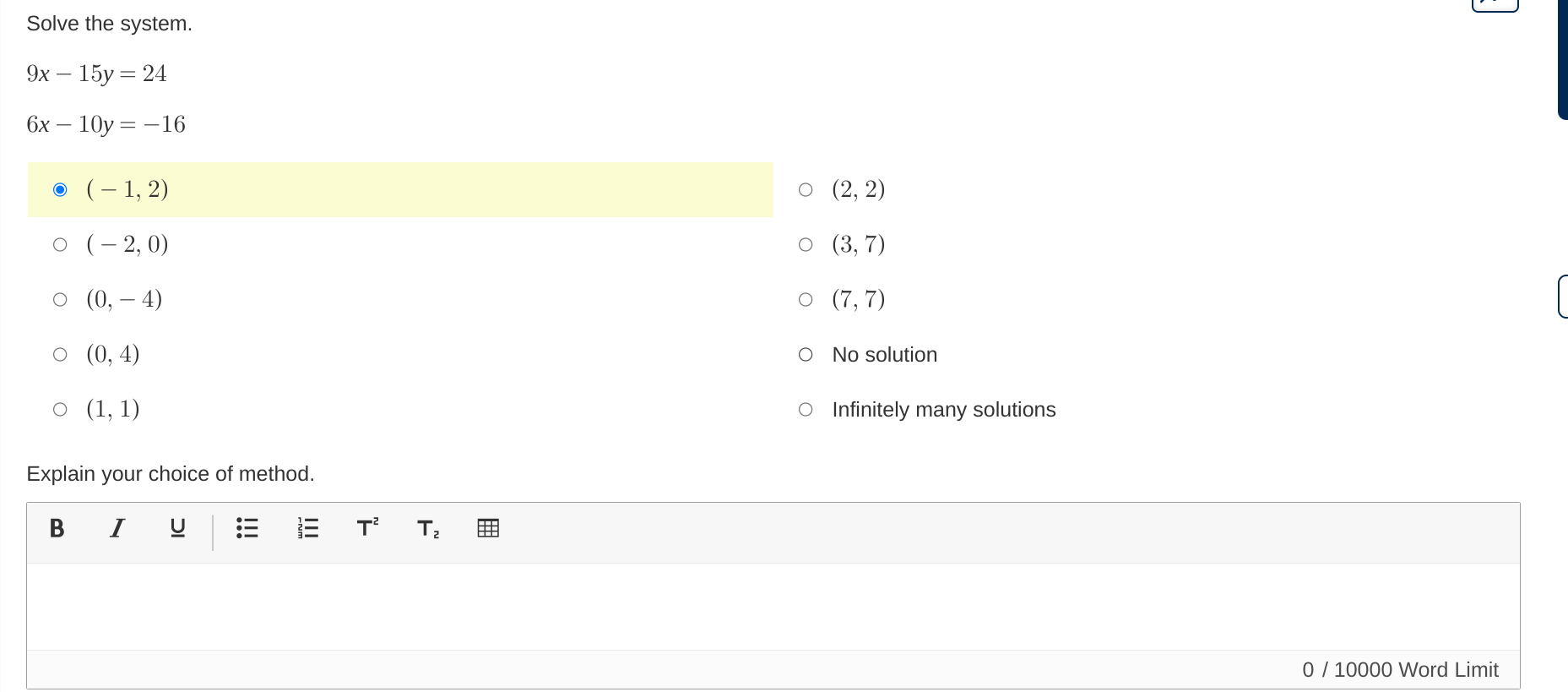
Solve the system. 9x - 15y = 24 and 6x - 10y = -16. Choose the correct solution from the options provided.

Understand the Problem

The question asks to solve a system of linear equations and choose an appropriate method for solving them. The user needs to determine the correct solution from the available options.

Answer

No solution

Steps to Solve

Write Down the Equations

The given equations are:

( 9x - 15y = 24 )
( 6x - 10y = -16 )

Simplify the Equations

We can simplify both equations.

For the first equation:

Divide every term by 3:

$$ 3x - 5y = 8 , , , \text{(Equation 1)} $$

For the second equation:

Divide every term by 2:

$$ 3x - 5y = -8 , , , \text{(Equation 2)} $$

Set the Equations Equal

Since both equations represent ( 3x - 5y ), we can set them equal:

$$ 8 = -8 $$

This shows that there is no possible solution because the equations represent parallel lines that never intersect.

Conclusion About the System

Since the two lines are parallel and do not intersect, we conclude that the system has "No solution".

No solution

More Information

This system of equations has no solution because the simplified equations represent two parallel lines in a graph. They don't intersect, meaning there are no values of ( x ) and ( y ) that satisfy both equations simultaneously.

Tips

Mixing up the signs when simplifying equations may lead to incorrect conclusions about the solution.
Assuming two equations are equivalent when they are actually parallel.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!