Solve the inequality x/4 + 2 ≥ 4.
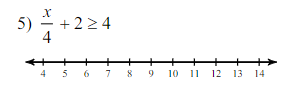
Understand the Problem
The question is asking us to solve the inequality x/4 + 2 ≥ 4 and represent the solution on a number line. We will isolate x to determine its range of values.
Answer
The solution is $x \geq 8$.
Answer for screen readers
The solution to the inequality is $x \geq 8$, represented as $[8, \infty)$ on the number line.
Steps to Solve
- Isolate the term with $x$
To begin, we need to subtract 2 from both sides of the inequality to isolate the term that contains $x$:
$$ \frac{x}{4} + 2 - 2 \geq 4 - 2 $$
This simplifies to:
$$ \frac{x}{4} \geq 2 $$
- Eliminate the fraction
Next, multiply both sides of the inequality by 4 to eliminate the fraction. Remember that since we are not multiplying or dividing by a negative number, the direction of the inequality remains the same:
$$ 4 \cdot \frac{x}{4} \geq 4 \cdot 2 $$
This simplifies to:
$$ x \geq 8 $$
- Express the solution
The solution tells us that $x$ must be greater than or equal to 8. In interval notation, this can be represented as $[8, \infty)$.
- Graph the solution on the number line
On the number line, place a closed dot on 8 to indicate that it is included in the solution and shade to the right to show that all values greater than 8 are included.
The solution to the inequality is $x \geq 8$, represented as $[8, \infty)$ on the number line.
More Information
This inequality indicates that any value of $x$ that is 8 or greater satisfies the original condition. Such inequalities often represent ranges of possible solutions in real-world scenarios, such as thresholds, limits, or minimum values.
Tips
- Incorrectly flipping the inequality: Remember that we only flip the inequality when multiplying or dividing by a negative number, which is not the case here.
- Confusing the boundary: Ensure to use a closed dot on the number line for values included in the solution (like 8) and an open dot for values not included.
AI-generated content may contain errors. Please verify critical information