Solve the inequality \( \frac{x}{4} + 2 \geq 4 \) and represent the solution on the number line.
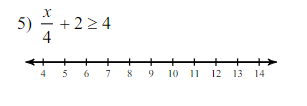
Understand the Problem
The question is asking to solve the inequality involving the variable x and present the solution on a number line. The approach will involve isolating x in the inequality and then determining the set of x values that satisfy the condition.
Answer
The solution is \( x \geq 8 \).
Answer for screen readers
The solution to the inequality is ( x \geq 8 ).
Steps to Solve
- Isolate the term with x
To solve the inequality ( \frac{x}{4} + 2 \geq 4 ), start by isolating the term with x. Subtract 2 from both sides:
$$ \frac{x}{4} \geq 4 - 2 $$
This simplifies to:
$$ \frac{x}{4} \geq 2 $$
- Eliminate the fraction
Next, multiply both sides by 4 to eliminate the fraction. Since 4 is positive, the direction of the inequality remains the same:
$$ x \geq 2 \times 4 $$
This simplifies to:
$$ x \geq 8 $$
- Represent on the number line
Now, we can represent the solution on the number line. Since ( x ) can take any value greater than or equal to 8, we will place a closed dot on 8 to indicate that it is included, and shade to the right to show all values greater than 8.
The solution to the inequality is ( x \geq 8 ).
More Information
This inequality shows that x can be any value starting from 8 and moving to positive infinity. The closed dot at 8 indicates that 8 is included in the solution set.
Tips
- Confusing inequality direction: Ensure to multiply or divide by positive numbers, as they do not change the inequality direction.
- Not including the boundary point: Remember that using ( \geq ) means including the boundary point in the solution.
AI-generated content may contain errors. Please verify critical information