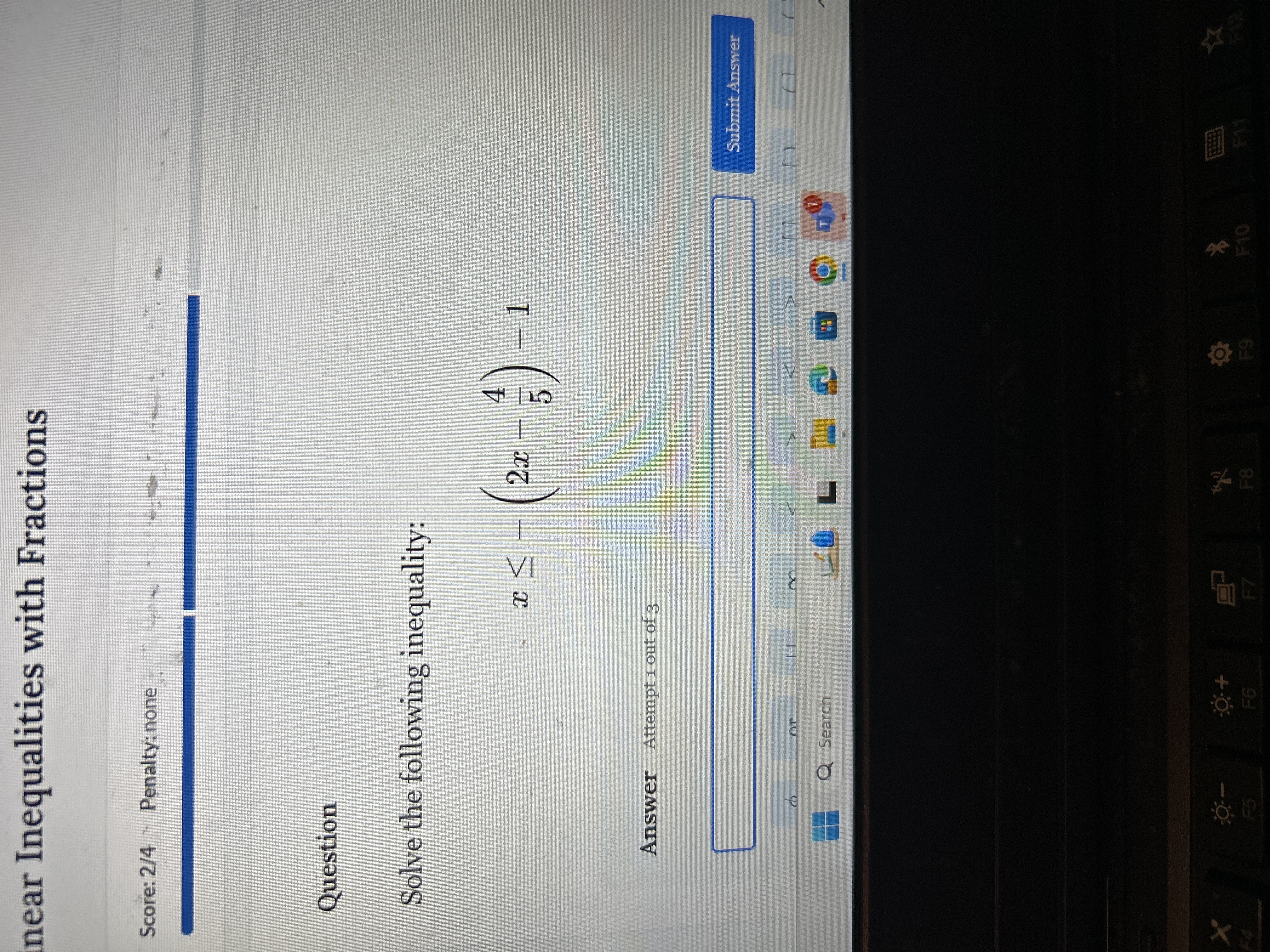
Solve the following inequality: x ≤ (2x - 4/5) - 1
Understand the Problem
The question is asking to solve the inequality involving a variable x, where it compares x to an expression containing another variable and fractional components. The goal is to isolate x and determine its range of values.
Answer
The solution to the inequality is \( x \geq \frac{9}{5} \).
Answer for screen readers
The solution to the inequality is: ( x \geq \frac{9}{5} ).
Steps to Solve
- Rewrite the Inequality
Start by rewriting the inequality for clarity: $$ x \leq \left(2x - \frac{4}{5}\right) - 1 $$
- Simplify the Right Side
Simplify the expression on the right: $$ x \leq 2x - \frac{4}{5} - 1 $$ To combine the constant terms, convert -1 to a fraction: $$ -1 = -\frac{5}{5} $$ Thus, $$ x \leq 2x - \frac{4}{5} - \frac{5}{5} $$ This simplifies to: $$ x \leq 2x - \frac{9}{5} $$
- Isolate x
Now, isolate $x$ by subtracting $2x$ from both sides: $$ x - 2x \leq -\frac{9}{5} $$ This simplifies to: $$ -x \leq -\frac{9}{5} $$
- Change the Direction of the Inequality
When you multiply or divide by a negative number, remember to flip the inequality: $$ x \geq \frac{9}{5} $$
The solution to the inequality is: ( x \geq \frac{9}{5} ).
More Information
The inequality states that ( x ) can take any value that is greater than or equal to ( 1.8 ) (since ( \frac{9}{5} = 1.8 )). This means all numbers from ( 1.8 ) to positive infinity are solutions.
Tips
- Not flipping the inequality: Remember to flip the inequality sign when multiplying or dividing by a negative number.
- Incorrect simplification: Ensure that fractions are combined correctly, as errors in basic arithmetic can lead to incorrect results.
AI-generated content may contain errors. Please verify critical information