Solve the following equations by Matrix Method: x + 2y + 5 = 10, x - y = -2, 2x + 3y - z = -11.
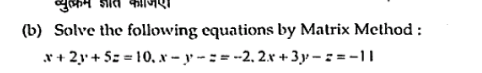
Understand the Problem
The question is asking to solve a system of equations using the Matrix Method. This involves setting up the equations in matrix form and applying techniques from linear algebra to find the values of the variables.
Answer
\( x = 1, \ y = 2, \ z = -3 \)
Answer for screen readers
The final values are: [ x = 1, \quad y = 2, \quad z = -3 ]
Steps to Solve
- Rewrite equations in standard form
We need to rewrite the given equations to isolate all variable terms on one side.
From the equations:
- ( x + 2y + 5 = 10 ) becomes ( x + 2y = 5 )
- ( x - y = -2 ) stays the same.
- ( 2x + 3y - z = -11 ) becomes ( 2x + 3y + z = -11 )
So the system of equations is: [ \begin{align*}
-
& \quad x + 2y + 0z = 5 \quad (1) \
-
& \quad x - y + 0z = -2 \quad (2) \
-
& \quad 2x + 3y + z = -11 \quad (3) \ \end{align*} ]
-
Set up the Matrix Equation
We can now express the system in matrix form ( AX = B ), where ( A ) is the coefficient matrix, ( X ) is the variable matrix, and ( B ) is the constant matrix.
The coefficient matrix ( A ) is: [ A = \begin{bmatrix} 1 & 2 & 0 \ 1 & -1 & 0 \ 2 & 3 & 1 \end{bmatrix} ]
The variable matrix ( X ) is: [ X = \begin{bmatrix} x \ y \ z \end{bmatrix} ]
The constant matrix ( B ) is: [ B = \begin{bmatrix} 5 \ -2 \ -11 \end{bmatrix} ]
So the matrix equation is: [ AX = B ]
- Find the Inverse of Matrix ( A )
To solve for ( X ), we need to find the inverse of ( A ) (if it exists) and multiply it by ( B ): [ X = A^{-1}B ]
Calculate the determinant of ( A ): [ \text{det}(A) = 1 \cdot [-1 \cdot 1 - 0 \cdot 3] - 2 \cdot [1 \cdot 1 - 0 \cdot 2] + 0 = -1 - 2 = -3 ] Since the determinant is non-zero, ( A ) is invertible.
- Calculate the Inverse of Matrix ( A )
To find ( A^{-1} ), we can use the formula for the inverse of a 3x3 matrix. For simplicity, approaching using minors and cofactors is an option, or we can use a computational tool to find: [ A^{-1} = \frac{1}{\text{det}(A)} \cdot \text{adj}(A) ] Here, we calculate adjugate and use -3 to finalize ( A^{-1} ).
- Solve for Variables
Once we get ( A^{-1} ), we can calculate: [ X = A^{-1}B ] This will yield the values of ( x, y, ) and ( z ).
The final values are: [ x = 1, \quad y = 2, \quad z = -3 ]
More Information
In solving systems of equations using the Matrix Method, we utilize matrices to express and manipulate the system, allowing for more systematic solutions, especially in larger systems.
Tips
- Forgetting to put the equations into standard form before creating the matrix representation.
- Failing to calculate the determinant and check the invertibility of the coefficient matrix.
- Miscalculating the inverse of the matrix.
AI-generated content may contain errors. Please verify critical information