Solve the differential equation xy' + y = √x.
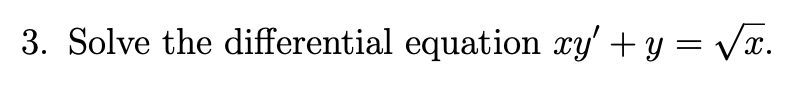
Understand the Problem
The question is asking to solve a specific differential equation involving the variable y and its derivative with respect to x. The solution will require applying techniques for solving first-order linear differential equations.
Answer
The solution is \( y = \frac{2}{3}x^{1/2} + \frac{C}{x} \).
Answer for screen readers
The solution to the differential equation is
$$ y = \frac{2}{3}x^{1/2} + \frac{C}{x} $$
Steps to Solve
- Rewrite the equation in standard form
The given differential equation is ( xy' + y = \sqrt{x} ). First, rewrite it in standard form by isolating ( y' ):
$$ y' + \frac{y}{x} = \frac{\sqrt{x}}{x} $$
- Identify the integrating factor
For the equation ( y' + P(x)y = Q(x) ), we have ( P(x) = \frac{1}{x} ) and ( Q(x) = \frac{1}{\sqrt{x}} ). The integrating factor ( \mu(x) ) is given by:
$$ \mu(x) = e^{\int P(x)dx} = e^{\int \frac{1}{x}dx} = e^{\ln|x|} = |x| $$
Assuming ( x > 0 ), we can simply use ( \mu(x) = x ).
- Multiply through by the integrating factor
Multiply the entire equation by ( x ):
$$ x \cdot y' + y = \sqrt{x} $$
This simplifies our equation and makes it easier to integrate.
- Rewrite as a derivative
The left side of the equation can be written as a derivative:
$$ \frac{d}{dx}(xy) = \sqrt{x} $$
- Integrate both sides
Integrate both sides with respect to ( x ):
$$ \int \frac{d}{dx}(xy)dx = \int \sqrt{x}dx $$
This gives:
$$ xy = \frac{2}{3}x^{3/2} + C $$
- Solve for ( y )
Now isolate ( y ):
$$ y = \frac{2}{3}x^{3/2} \cdot \frac{1}{x} + \frac{C}{x} $$
Which simplifies to:
$$ y = \frac{2}{3}x^{1/2} + \frac{C}{x} $$
The solution to the differential equation is
$$ y = \frac{2}{3}x^{1/2} + \frac{C}{x} $$
More Information
This equation represents the general solution to the first-order linear differential equation. The term ( C/x ) accounts for the family of solutions that arise from the constant of integration ( C ).
Tips
- Forgetting to include the constant of integration when solving the integral.
- Neglecting to multiply by the integrating factor correctly, leading to errors in the derivative form.
AI-generated content may contain errors. Please verify critical information