Solve the differential equation (x^4 - 2xy^2 + y^4) dx - (2x^2y - 4xy^3 + sin y) dy = 0.
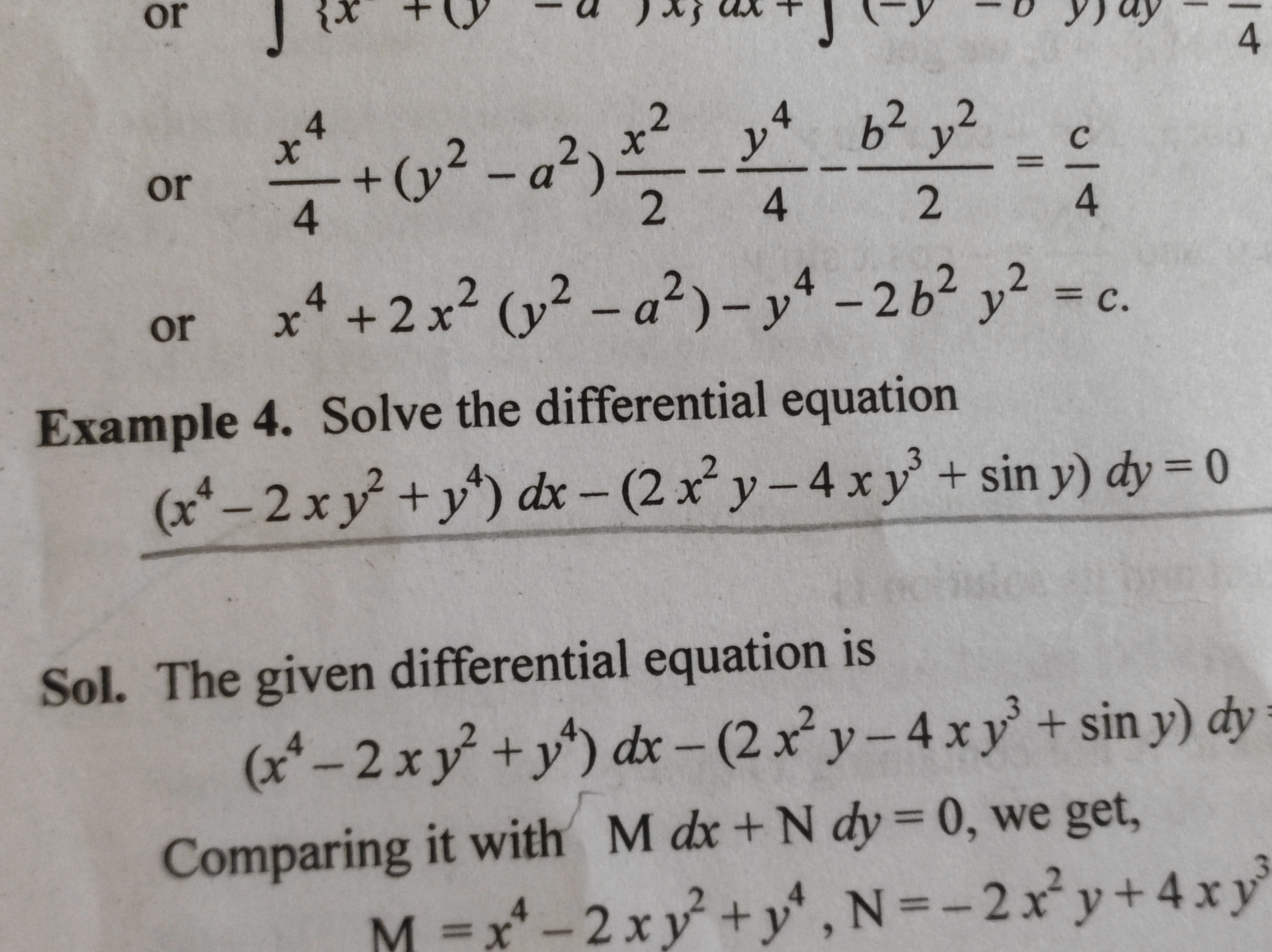
Understand the Problem
The question is asking to solve a specific differential equation. The user presents the equation in a mathematical form and expects a solution or method to solve it.
Answer
The solution to the differential equation is given by the function \( \psi(x, y) = C \), derived from integrating \( M \) and \( N \).
Answer for screen readers
The final answer will be the function ( \psi(x, y) = C ) after completing the integration and substitution steps.
Steps to Solve
-
Identify the differential equation The given equation is $$(x^4 - 2xy^2 + y^4)dx - (2x^2y - 4xy^3 + \sin y)dy = 0.$$ We can compare it to the standard form ( M dx + N dy = 0 ) where: $$ M = x^4 - 2xy^2 + y^4 $$ $$ N = - (2x^2y - 4xy^3 + \sin y) $$
-
Check for exactness To determine if the differential equation is exact, we need to verify if $$ \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}. $$
Calculate ( \frac{\partial M}{\partial y} ): $$ \frac{\partial M}{\partial y} = -4xy + 4y^3 $$
Now calculate ( \frac{\partial N}{\partial x} ): $$ \frac{\partial N}{\partial x} = - (4xy - 2x^2) $$
You can simplify and compare these results.
-
Integrate M with respect to x If the equation is exact, integrate ( M ) with respect to ( x ): $$ \psi(x, y) = \int (x^4 - 2xy^2 + y^4)dx = \frac{x^5}{5} - x^2y^2 + xy^4 + g(y) $$ where ( g(y) ) is an arbitrary function of ( y ).
-
Differentiate with respect to y Differentiate ( \psi(x, y) ) with respect to ( y ): $$ \frac{\partial \psi}{\partial y} = -2xy + 4xy^3 + g'(y) $$
-
Set equal to N Equate this to ( N ) to find ( g'(y) ): $$ -2xy + 4xy^3 + g'(y) = - (2x^2y - 4xy^3 + \sin y) $$ Solve for ( g'(y) ) and integrate to find ( g(y) ).
-
Combine results The final solution can be written as: $$ \psi(x, y) = C $$ where ( C ) is a constant. Substitute ( g(y) ) and ( \psi(x, y) ) back to form the complete solution.
The final answer will be the function ( \psi(x, y) = C ) after completing the integration and substitution steps.
More Information
This differential equation involves methods of finding exact solutions through comparison and integration. Understanding exact equations helps solve various types of differential problems in mathematics.
Tips
- Not checking for exactness before proceeding.
- Forgetting to include an arbitrary function during integration.
- Miscalculating derivatives.